(本小題滿分12分)
如圖,三棱柱
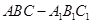
中,
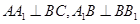
.

(1)求證:
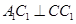
;
(2)若
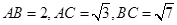
,問
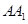
為何值時,三棱柱
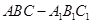
體積最大,并求此最大值。
試題分析:(1)證明線線垂直,一般利用線面垂直判定及性質定理進行多次轉化證明. 由
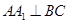
知
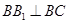
,又
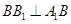
,故
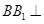
平面
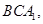
即
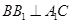
,又
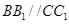
,所以
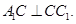
(2)研究三棱柱體積,關鍵明確底面上的高,本題由(1)知:
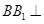
平面
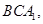
因此將三棱柱體積轉化為等高同底的三棱錐
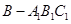
體積(三倍關系),而三棱錐
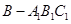
體積又等于三棱錐
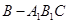
體積,三棱錐
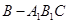
體積等于
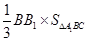
,設
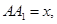
不難計算
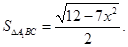
三棱柱
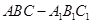
的體積為
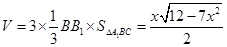
,故當
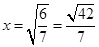
時,即
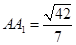
時,體積
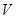
取到最大值
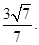
試題解析:
(1)證明:由
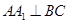
知
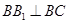
,又
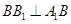
,故
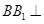
平面
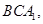
即
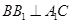
,又
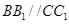
,所以
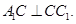
(2)設
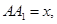
在

中

同理
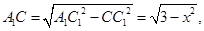
在
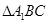
中,
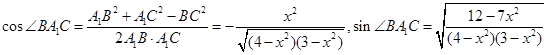
,所以
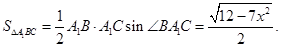
從而三棱柱
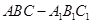
的體積為
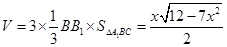
因
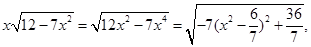
故當
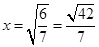
時,即
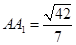
時,體積
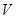
取到最大值
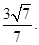
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在平行四邊形
中,
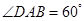
,
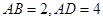
,將

沿
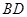
折起到
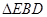
的位置.
(1)求證:

平面

;
(2)當
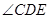
取何值時,三棱錐
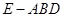
的體積取最大值?并求此時三棱錐
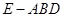
的側面積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
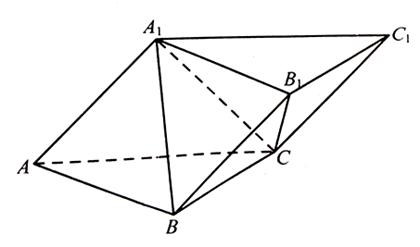
在斜三棱柱
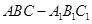
中,平面
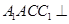
平面ABC,
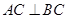
,
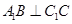
,
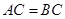
.
(1)求證:
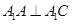
;
(2)若
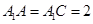
,求三棱錐
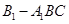
的體積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
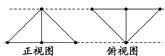
把邊長為1的正方形ABCD沿對角線BD折起,形成的三棱錐C-ABD,其正視圖與俯視圖如圖所示,則側視圖的面積為______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列關于用斜二測畫法畫直觀圖的說法中,錯誤的是( )
| A.用斜二測畫法畫出的直觀圖是在平行投影下畫出的空間圖形 |
| B.幾何體的直觀圖的長、寬、高與其幾何體的長、寬、高的比例相同 |
| C.水平放置的矩形的直觀圖是平行四邊形 |
| D.水平放置的圓的直觀圖是橢圓 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
兩球的體積之比為8:1,則它們的表面積之比為( )
| A.8:1 | B.4:1 | C.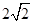 :1 :1 | D.2:1 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設甲,乙兩個圓柱的底面面積分別為
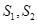
,體積為
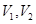
,若它們的側面積相等且
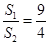
,則
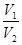
的值是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
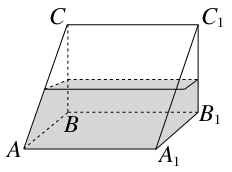
如圖,一個封閉的三棱柱容器中盛有水,且側棱長AA
1=8.若側面AA
1B
1B水平放置時,液面恰好經(jīng)過AC,BC,A
1C
1,B
1C
1的中點. 當?shù)酌鍭BC水平放置時,液面高度為________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
三角形
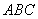
中,
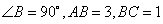
,以邊
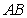
所在直線為旋轉軸,其余各邊旋轉一周而形成的曲面所圍成的幾何體的體積為( )
查看答案和解析>>

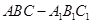 中,
中,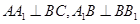 .
.
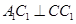 ;
;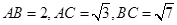 ,問
,問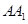 為何值時,三棱柱
為何值時,三棱柱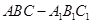 體積最大,并求此最大值。
體積最大,并求此最大值。 閱讀快車系列答案
閱讀快車系列答案