中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知f(z)＝|1＋z|－，且f(－x)＝10＋3i，則復數z＝_________．

答案：5－3i
解析：

　　設z＝x＋yi(x、y∈R)，

　　則－z＝－x－yi，由f(－z)＝10＋3i，得

　　|1＋(－z)|－()＝10＋3i，

　　|(1－x)－yi|－(－x＋yi)＝10＋3i，

　　∴

　　解之，得x＝5，y＝－3．

　　∴所求z＝5－3i．


練習冊系列答案
相關習題

科目：高中數學 來源：成功之路·突破重點線·數學（學生用書） 題型：044

已知f(x)＝＋，并且x≠2kπ＋，k∈Z；．

(1)化簡f(x)；

(2)是否存在x，使得tan·f(x)與相等？若存在，求x的值；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源：吉林省長春外國語學校2008-2009學年高二下學期第一次月考數學試卷 題型：044

已知f(z)＝|1＋z|－，且f(－z)＝10＋3i，求復數z．

查看答案和解析>>

科目：高中數學 來源：學習周報　數學　北師大課標高二版(選修1－2)　2009－2010學年　第38期　總第194期 北師大課標 題型：044

已知f(z)＝|1＋z|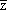－，且f(－z)＝10＋3i，求復數z．

查看答案和解析>>

科目：高中數學 來源：吉林省長春外國語學校2012屆高三上學期期中考試數學文科試題 題型：044

已知函數y＝f(x)的定義域為R，對任意的x，y∈R，都有f(x＋y)＝f(x)＋f(y)，對任意的x＞0，都有f(x)＜0，且f(3)＝－3

(1)證明函數y＝f(x)在R上是減函數．

(2)證明函數y＝f(x)是奇函數．

(3)試求y＝f(x)在區間[m，n](m，n∈Z且mn＜0)上的值域．

查看答案和解析>>

同步練習冊答案