
定義在R上的函數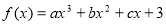 同時滿足以下條件:
同時滿足以下條件:
①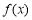 在(0,1)上是減函數,在(1,+∞)上是增函數;
在(0,1)上是減函數,在(1,+∞)上是增函數;
② 是偶函數;
是偶函數;
③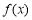 在x=0處的切線與直線y=x+2垂直.
在x=0處的切線與直線y=x+2垂直.
(1)求函數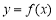 的解析式;
的解析式;
(2)設g(x)=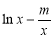 ,若存在實數x∈[1,e],使g(x)<
,若存在實數x∈[1,e],使g(x)< ,求實數m的取值范圍。
,求實數m的取值范圍。
(1) f(x)=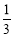 x3 x+3, (2) m>2e e3
x3 x+3, (2) m>2e e3
【解析】
試題分析:(1)三個條件,三個未知數,本題就是通過條件列方程組解參數,第一個條件說的是單調性,實質是導數,即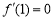 ,3a+2b+c=0;第二個條件是函數的奇偶性,利用
,3a+2b+c=0;第二個條件是函數的奇偶性,利用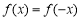 恒成立即可,b=0;第三個條件是導數幾何意義,即
恒成立即可,b=0;第三個條件是導數幾何意義,即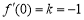 , c= 1 ;因此
, c= 1 ;因此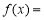
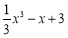 ;(2)存在型問題,轉化為函數最值,首先進行變量分離,即m>xlnx x3+x,然后求函數M(x)=xlnx x3+x在[1,e]上最小值,這又要利用導數研究函數M(x)在[1,e]上的單調性,分析得為M(x)在[1,e]上遞減,所以M(x)最小值為M(e)=2e e3于是有m>2e e3
;(2)存在型問題,轉化為函數最值,首先進行變量分離,即m>xlnx x3+x,然后求函數M(x)=xlnx x3+x在[1,e]上最小值,這又要利用導數研究函數M(x)在[1,e]上的單調性,分析得為M(x)在[1,e]上遞減,所以M(x)最小值為M(e)=2e e3于是有m>2e e3
試題解析:【解析】
(1)f′(x)=3ax2+2bx+c,∵f(x)在(0,1)上是減函數,在(1,+∞)上是增函數,
∴f′(1)=3a+2b+c=0 ①
由f′(x)是偶函數得:b=0 ②
又f(x)在x=0處的切線與直線y=x+2垂直,f′(0)=c= 1 ③
由①②③得:a=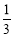 ,b=0,c= 1,即
,b=0,c= 1,即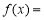
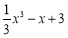 . 4分
. 4分
(2)由已知得:存在實數x∈[1,e],使lnx 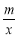 <x2 1
<x2 1
即存在x∈[1,e],使m>xlnx x3+x 6分
設M(x)=xlnx x3+x,x∈[1,e],則M′(x)=lnx 3x2+2 8分
設H(x)=lnx 3x2+2,則H′(x)=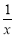 6x=
6x=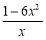 10分
10分
∴M(x)在[1,e]上遞減,
∵x∈[1,e],∴H′(x)<0,即H(x)在[1,e]上遞減
于是,H(x)≤H(1),即H(x)≤ 1<0,即M′(x)<0
∴M(x)≥M(e)=2e e3
于是有m>2e e3為所求. 12分
考點:導數在函數中的應用


科目:高中數學 來源:2015屆浙江溫州十校聯合體高二上學期期末聯考文數學卷(解析版) 題型:選擇題
設 是兩條不同的直線,
是兩條不同的直線, 是三個不同的平面,下列四個命題中假命題的是( )
是三個不同的平面,下列四個命題中假命題的是( )
A.若 則
則 B.若
B.若 則
則
C.若 則
則 D.若
D.若 ,則
,則
查看答案和解析>>
科目:高中數學 來源:2015屆河南許昌市五高二上期期末聯考理科數學試卷(解析版) 題型:選擇題
已知橢圓 和雙曲線
和雙曲線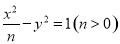 有相同的焦點
有相同的焦點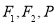 是它們的一個交點,則
是它們的一個交點,則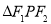 的形狀是( )
的形狀是( )
A. 銳角三角形 B. 直角三角形
C. 鈍角三角形 D. 隨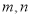 的變化而變化
的變化而變化
查看答案和解析>>
科目:高中數學 來源:2015屆河南許昌市五高二上期期末聯考理科數學試卷(解析版) 題型:選擇題
“ ”是“直線
”是“直線 與直線
與直線 相互垂直”的 ( )
相互垂直”的 ( )
A. 充分必要條件 B. 充分而不必要條件
C. 必要而不充分條件 D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2015屆河南許昌市五高二上期期末聯考文科數學試卷(解析版) 題型:填空題
下列結論中 ①函數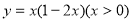 有最大值
有最大值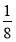 ②函數
②函數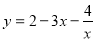 (
( )有最大值
)有最大值 ③若
③若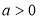 ,則
,則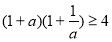 正確的序號是_____________.
正確的序號是_____________.
查看答案和解析>>
科目:高中數學 來源:2015屆江西贛州四所重點中學高二上學期期末聯考理數學試卷(解析版) 題型:填空題
如圖,正方體ABCD—A1B1C1D1,

則下列四個命題:
①P在直線BC1上運動時,三棱錐A—D1PC的體積不變;
②P在直線BC1上運動時,直線AP與平面ACD1所成角的大小不變;
③P在直線BC1上運動時,二面角P—AD1—C的大小不變;
④M是平面A1B1C1D1上到點D和C1距離相等的點,則M點的軌跡是過D1點的直線D1A1。
其中真命題的編號是 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com