
“中國式過馬路”存在很大的交通安全隱患.某調查機構為了解路人對“中國式過馬路”的態度是否與性別有關,從馬路旁隨機抽取30名路人進行了問卷調查,得到了如下列聯表:
| | 男性 | 女性 | 合計 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合計 | | | 30 |
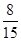 .
.| P(K2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
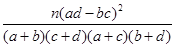 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)"  新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
將編號為1,2,3,4的四個小球,分別放入編號為1,2,3,4的四個盒子,每個盒子中有且僅有一個小球.若小球的編號與盒子的編號相同,得1分,否則得0分.記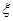 為四個小球得分總和.
為四個小球得分總和.
(1)求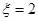 時的概率;
時的概率;
(2)求 的概率分布及數學期望.
的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某校高三畢業班報考體育專業學生的體重(單位:千克)情況,將從該市某學校抽取的樣本數據整理后得到如下頻率分布直方圖.已知圖中從左至右前3個小組的頻率之比為1:2:3,其中第2小組的頻數為12.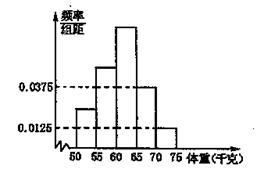
(Ⅰ)求該校報考體育專業學生的總人數n;
(Ⅱ)若用這所學校的樣本數據來估計該市的總體情況,現從該市報考體育專業的學生中任選3人,設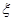 表示體重超過60千克的學生人數,求
表示體重超過60千克的學生人數,求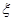 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某射手每次射擊擊中目標的概率均為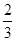 ,且每次射擊的結果互不影響
,且每次射擊的結果互不影響
(I)假設這名射手射擊3次,求至少2次擊中目標的概率
(II)假設這名射手射擊3次,每次擊中目標10分,未擊中目標得0分,在3次射擊中,若有兩次連續擊中目標,而另外一次未擊中目標,則額外加5分;若3次全部擊中,則額外加10分。用隨機變量§表示射手射擊3次后的總得分,求§的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關.現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,在將兩組工人的日平均生產件數分成5組: 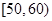 ,
, ,
,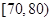 ,
,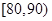 ,
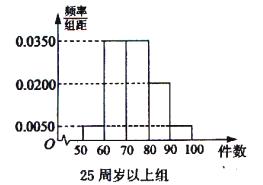
,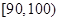 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.
(1)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的頻率.
(2)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成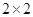 的列聯表,并判斷是否有
的列聯表,并判斷是否有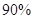 的把握認為“生產能手與工人所在的年齡組有關”?
的把握認為“生產能手與工人所在的年齡組有關”?
附表:
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩位籃球運動員進行定點投籃,甲投籃一次命中的概率為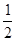 ,乙投籃一次命中的概率為
,乙投籃一次命中的概率為 .每人各投4個球,兩人投籃命中的概率互不影響.
.每人各投4個球,兩人投籃命中的概率互不影響.
(1)求甲至多命中1個球且乙至少命中1個球的概率;
(2)若規定每投籃一次命中得3分,未命中得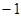 分,求乙所得分數
分,求乙所得分數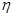 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某人在如圖所示的直角邊長為4米的三角形地塊的每個格點(指縱、橫直線的交叉點以及三角形的頂點)處都種了一株相同品種的作物。根據歷年的種植經驗,一株該種作物的年收貨量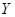 (單位:kg)與它的“相近”作物株數
(單位:kg)與它的“相近”作物株數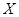 之間的關系如下表所示:
之間的關系如下表所示: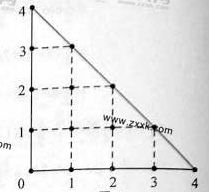
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
| Y | 51 | 48 | 45 | 42 |
| 頻數 | | 4 | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
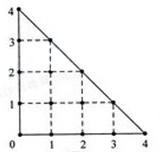
某人在如圖所示的直角邊長為4米的三角形地塊的每個格點(指縱、橫的交叉點記憶三角形的頂點)處都種了一株相同品種的作物。根據歷年的種植經驗,一株該種作物的年收獲量Y(單位:kg)與它的“相近”作物株數X之間的關系如下表所示:
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
山東省某示范性高中為了推進新課程改革,滿足不同層次學生的需求,決定從高一年級開始,在每周的周一、周三、周五的課外活動期間同時開設數學、物理、化學、生物和信息技術輔導講座,每位有興趣的同學可以在期間的任何一天參加任何一門科目的輔導講座,也可以放棄任何一門科目的輔導講座.(規定:各科達到預先設定的人數時稱為滿座,否則稱為不滿座)統計數據表明,各學科講座各天的滿座概率如下表:
| | 信息技術 | 生物 | 化學 | 物理 | 數學 |
| 周一 | 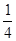 | 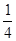 | 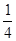 | 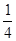 |  |
| 周三 |  |  |  |  | 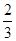 |
| 周五 |  |  |  |  | 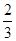 |
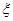 ,求隨即變量
,求隨即變量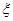 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com