已知函數(shù)
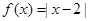
(1)解不等式
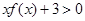
;
(2)對于任意的
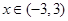
,不等式
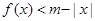
恒成立,求
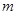
的取值范圍.
(1)
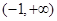
;(2)
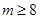
.
試題分析:本題考查絕對值不等式的解法和不等式的恒成立問題,考查學生的分類討論思想和轉(zhuǎn)化能力.第一問,利用零點分段法進行分類求解;第二問,利用函數(shù)的單調(diào)性求出最大值證明恒成立問題.
試題解析:(1)
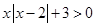
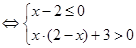
或
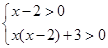
3分
解得
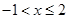
或
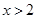
∴不等式解集為
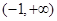
6分
(2)
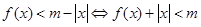
,即
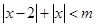
, 7分
設
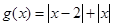
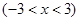
,則
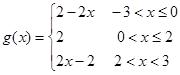
9分
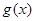
在
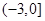
上單調(diào)遞減,
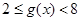
;
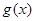
在
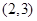
上單調(diào)遞增,
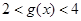
∴在
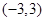
上
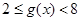
, 11分
故
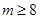
時不等式
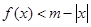
在
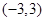
上恒成立 12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
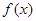
的定義域為
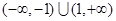
,對定義域內(nèi)的任意x,滿足
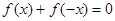
,當
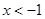
時,
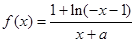
(a為常),且
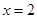
是函數(shù)
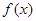
的一個極值點,
(1)求實數(shù)a的值;
(2)如果當
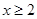
時,不等式
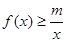
恒成立,求實數(shù)m的最大值;
(3)求證:
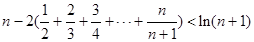
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
某社區(qū)有甲、乙兩家乒乓球俱樂部,兩家設備和服務都很好,但收費方式不同.甲家每張球臺每小時5元;乙家按月計費,一個月中30小時以內(nèi)(含30小時)每張球臺90元,超過30小時的部分每張球臺每小時2元.小張準備下個月從這兩家中的一家租一張球臺開展活動,其活動時間不少于15小時,也不超過40小時.
(1)設在甲家租一張球臺開展活動
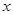
小時的收費為
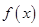
元
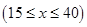
,在乙家租一張球臺開展活動
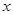
小時的收費為
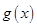
元
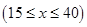
.試求
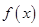
和
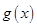
.
(2)問:小張選擇哪家比較合算?為什么?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
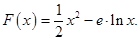
(I)求函數(shù)
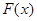
的極值;
(II)對于函數(shù)
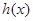
和
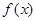
定義域內(nèi)的任意實數(shù)
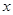
,若存在常數(shù)
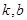
,使得不等式
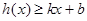
和
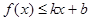
都成立,則稱直線
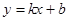
是函數(shù)
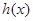
和
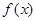
的“分界線”.
設函數(shù)
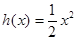
,
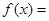
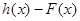
,試問函數(shù)
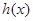
和
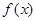
是否存在“分界線”?若存在,求出“分界線”的方程.若不存在請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設a> 0,a≠ 1,若y = a
x的反函數(shù)的圖象經(jīng)過點
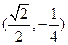
,則a=
| A.16 | B.2 | C.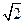 | D.4 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在同一坐標系中,函數(shù)y=ax+1與y=a
|x-1|(a>0且a≠1)的圖象可能是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設函數(shù)
f(
x)的定義域為
D,若存在非零實數(shù)
l使得對于任意
x∈
M(
M⊆
D),有
x+
l∈
D,且
f(
x+
l)≥
f(
x),則稱函數(shù)
f(
x)為
M上的
l高調(diào)函數(shù).現(xiàn)給出下列命題:
①函數(shù)
f(
x)=
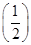 x
x是R上的1高調(diào)函數(shù);
②函數(shù)
f(
x)=sin 2
x為R上的π高調(diào)函數(shù);
③如果定義域為[-1,+∞)的函數(shù)
f(
x)=
x2為[-1,+∞)上的
m高調(diào)函數(shù),那么實數(shù)
m的取值范圍是[2,+∞).
其中正確的命題是________.(寫出所有正確命題的序號)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,公園有一塊邊長為2的等邊△ABC的邊角地,現(xiàn)修成草坪,圖中

把草坪分成面積相等的兩部分,

在

上,

在

上.

(1)設

,求用

表示

的函數(shù)關系式;
(2)如果

是灌溉水管,為節(jié)約成本,希望它最短,

的位置應在哪里?如果

是參觀線路,則希望它最長,

的位置又應在哪里?請說明理由.
查看答案和解析>>

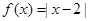
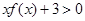 ;
;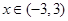 ,不等式
,不等式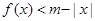 恒成立,求
恒成立,求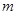 的取值范圍.
的取值范圍. 閱讀快車系列答案
閱讀快車系列答案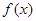 的定義域為
的定義域為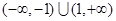 ,對定義域內(nèi)的任意x,滿足
,對定義域內(nèi)的任意x,滿足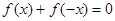 ,當
,當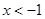 時,
時,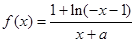 (a為常),且
(a為常),且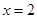 是函數(shù)
是函數(shù)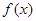 的一個極值點,
的一個極值點,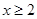 時,不等式
時,不等式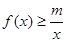 恒成立,求實數(shù)m的最大值;
恒成立,求實數(shù)m的最大值;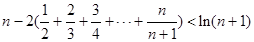
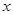 小時的收費為
小時的收費為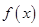 元
元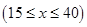 ,在乙家租一張球臺開展活動
,在乙家租一張球臺開展活動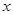 小時的收費為
小時的收費為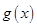 元
元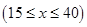 .試求
.試求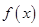 和
和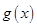 .
.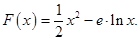
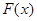 的極值;
的極值;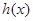 和
和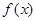 定義域內(nèi)的任意實數(shù)
定義域內(nèi)的任意實數(shù)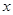 ,若存在常數(shù)
,若存在常數(shù)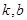 ,使得不等式
,使得不等式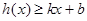 和
和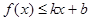 都成立,則稱直線
都成立,則稱直線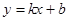 是函數(shù)
是函數(shù)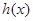 和
和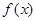 的“分界線”.
的“分界線”.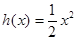 ,
,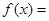
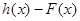 ,試問函數(shù)
,試問函數(shù)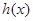 和
和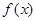 是否存在“分界線”?若存在,求出“分界線”的方程.若不存在請說明理由.
是否存在“分界線”?若存在,求出“分界線”的方程.若不存在請說明理由.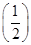 x是R上的1高調(diào)函數(shù);
x是R上的1高調(diào)函數(shù); 把草坪分成面積相等的兩部分,
把草坪分成面積相等的兩部分, 在
在 上,
上, 在
在 上.
上.
 ,求用
,求用 表示
表示 的函數(shù)關系式;
的函數(shù)關系式; 是灌溉水管,為節(jié)約成本,希望它最短,
是灌溉水管,為節(jié)約成本,希望它最短, 的位置應在哪里?如果
的位置應在哪里?如果 是參觀線路,則希望它最長,
是參觀線路,則希望它最長, 的位置又應在哪里?請說明理由.
的位置又應在哪里?請說明理由.