Question

某工廠生產甲、乙兩種產品，每種產品都是經過第一和第二工序加工而成，兩道工序的加工結果相互獨立，每道工序的加工結果均有A、B兩個等級.對每種產品，兩道工序的加工結果都為A級時，產品為一等品，其余均為二等品.

（1）已知甲、乙兩種產品每一道工序的加工結果為A級的概率如表一所示，分別求生產出的甲、乙產品為一等品的概率P_甲、P_乙；

（2）已知一件產品的利潤如表二所示，用ξ、η分別表示一件甲、乙產品的利潤，在（1）的條件下，求ξ、η的分布列及Eξ、Eη；

（3）已知生產一件產品需用的工人數和資金額如表三所示.該工廠有工人40名，可用資金60萬元.設x、y分別表示生產甲、乙產品的數量，在（2）的條件下，x、y為何值時，z=xEξ+yEη最大？最大值是多少？（解答時須給出圖示）

表一

Answer 1

思路解析：本題主要綜合考查了相互獨立事件的概率、隨機變量的分布列及期望、線性規劃模型的建立與求解等知識.可以通過建立一個簡單的數學模型來解決.

解：（1）P_甲=0.8×0.85=0.68,  P_乙=0.75×0.8=0.6.

（2）隨機變量ξ、η的分別列是

ξ	5	2.5
P	0.68	0.32

 

η	2.5	1.5
P	0.6	0.4

Eξ=5×0.68+2.5×0.32=4.2,

Eη=2.5×0.6+1.5×0.4=2.1.

（3）由題設知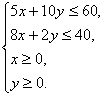

目標函數為z=xEξ+yEη=4.2x+2.1y.

作出可行域（如下圖）：作直線l:4.2x+2.1y=0，得l向右上方平移l₁位置時，直線經過可行

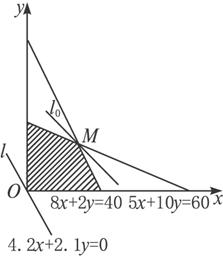
城上點M，點與原點距離最大，此時Z=4.2x+2.1y取最大值.

解方程組

得x=4,y=4.

即x=4,y=4時，z取最大值，z的最大值為25.2.