在正方體ABCD—A
1B
1C
1D
1中,M、N、P、Q分別是棱AB、BC、CD、CC
1的中點,直線MN與PQ所成的度數(shù)是 ( )
A.
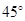
B.
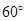
C.
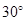
D.
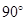
試題分析:連接DC
1,A
1C
1,因為M、N、P、Q分別是棱AB、BC、CD、CC
1的中點,
所以MN// A
1C
1,PQ// DC
1,MN與PQ所成的度數(shù)等于A
1C
1, DC
1所成角的度數(shù)為
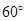
,
故選B。
點評:簡單題,空間問題往往要轉化成平面問題,特別是角,轉化成在同一四邊形、三角形內。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在直角梯形ABCD中,AD//BC,∠ADC=90º,AE⊥平面ABCD,EF//CD,BC=CD=AE=EF=

=1.

(Ⅰ)求證:CE//平面ABF;
(Ⅱ)求證:BE⊥AF;
(Ⅲ)在直線BC上是否存在點M,使二面角E-MD-A的大小為
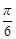
?若存在,求出CM的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在圓錐
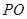
中,已知
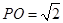
,⊙O的直徑
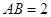
,
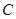
是
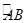
的中點,
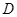
為
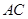
的中點.
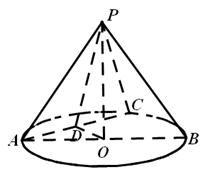
(1)證明:平面
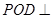
平面
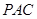
;
(2)求二面角
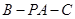
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,△ABC中,∠ACB=90°,直線l過點A且垂直于平面ABC,動點P∈l,當點P逐漸遠離點A時,∠PCB的大小( ).

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,正方體ABCD—A
1B
1C
1D
1中,E為AB中點,F(xiàn)為正方形BCC
1B
1的中心.

(1)求直線EF與平面ABCD所成角的正切值;
(2)求異面直線A
1C與EF所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,二面角
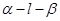
的大小是60°,線段
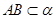
.
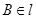
,
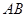
與
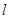
所成的角為30°.則
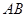
與平面
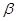
所成的角的正弦值是
.
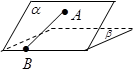
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
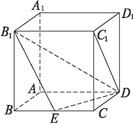
已知棱長為a的正方體ABCD—A
1B
1C
1D
1,E為BC中點.
(1)求B到平面B
1ED距離
(2)求直線DC和平面B
1ED所成角的正弦值. (12分)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知異面直線
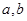
所成的角為
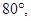
過空間一點O與
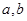
所成的角都是
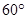
的直線有___________條
查看答案和解析>>

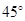 B.
B.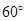 C.
C.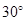 D.
D.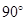
 輕松暑假總復習系列答案
輕松暑假總復習系列答案 =1.
=1.
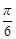 ?若存在,求出CM的長;若不存在,請說明理由.
?若存在,求出CM的長;若不存在,請說明理由.

