
已知函數![]() .
.
(1)若方程![]() 在區間
在區間![]() 內有兩個不相等的實根,求實數
內有兩個不相等的實根,求實數![]() 的取值范圍;
的取值范圍;
(2)如果函數![]() 的圖像與x軸交于兩點
的圖像與x軸交于兩點![]() ,且
,且![]() ,求證:
,求證:![]() (其中,
(其中,![]() 是
是![]() 的導函數,正常數
的導函數,正常數![]() 滿足
滿足![]() ).
).
解:(1)∵![]() ,
,![]() , -----1分
, -----1分
∴當![]() 時,
時,![]() ,
,![]() 單調遞增;當
單調遞增;當![]() 時,
時,![]() ,
,![]() 單調遞減。 ----3分
單調遞減。 ----3分
∴當x=1時,![]() 有極大值,也是最大值,即為-1,但無最小值。
有極大值,也是最大值,即為-1,但無最小值。
故![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;最大值為-1,但無最小值。
;最大值為-1,但無最小值。
方程化為![]() , -----3分
, -----3分
由上知,![]() 在區間
在區間![]() 上的最大值為-1,
上的最大值為-1,![]() ,
,![]() ,
,![]() 。故
。故![]() 在區間
在區間![]() 上有兩個不等實根需滿足
上有兩個不等實根需滿足![]() ,
,
∴![]() ,∴實數m的取值范圍為
,∴實數m的取值范圍為![]() 。 -----6分
。 -----6分
(2)∵![]() ,又
,又![]() 有兩個實根
有兩個實根![]() ,
,
∴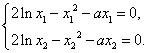 兩式相減,得
兩式相減,得![]()
∴![]() -----8分
-----8分
于是![]()
=![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() 。 -----9分
。 -----9分
要證:![]() ,只需證:
,只需證:![]() .
.
只需證:![]() . (*)
. (*)
令![]() ,∴(*)化為
,∴(*)化為![]()
只證![]() 即可. -----11分
即可. -----11分
![]()
![]()
![]()
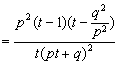 ,
,![]() ,0<t<1,
,0<t<1,
∴t-1<0.
∴u'(t)>0,∴u(t)在(0,1)上單調遞增,∴u(t)<u(1)=0
∴u(t)<0,![]()
即:![]() .
.
![]() .............13分
.............13分


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數學 來源:2012-2013學年湖南省岳陽市高三第一次質量檢測理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數
 .
.
(1)若 為
為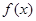 的極值點,求實數
的極值點,求實數 的值;
的值;
(2)若 在
在 上為增函數,求實數
上為增函數,求實數 的取值范圍;
的取值范圍;
(3)當 時,方程
時,方程 有實根,求實數
有實根,求實數 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源:吉林省10-11學年高二下學期期末考試數學(理) 題型:解答題
已知函數 .
.
(1)若從集合 中任取一個元素
中任取一個元素 ,從集合
,從集合 中任取一個元素
中任取一個元素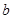 ,求方程
,求方程 有兩個不相等實根的概率;
有兩個不相等實根的概率;
(2)若 是從區間
是從區間 中任取的一個數,
中任取的一個數,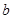 是從區間
是從區間 中任取的一個數,求方程
中任取的一個數,求方程 沒有實根的概率.
沒有實根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com