Question

由直線y=x與曲線y=x²所圍圖形的面積S=________．

Answer 1

分析：先根據題意畫出區域，然后依據圖形得到積分下限為0，積分上限為1，從而利用定積分表示出曲邊梯形的面積，最后用定積分的定義求出所求即可．
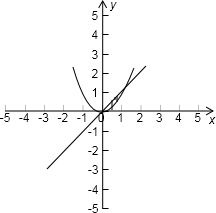
解答：先根據題意畫出圖形，得到積分上限為1，積分下限為0
直線y=x與曲線y=x²所圍圖形的面積S=∫₀¹（x-x²）dx
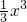
而∫₀³（x-x²）dx=（-）|₀¹=-=
∴曲邊梯形的面積是
故答案為：．
點評：本題主要考查了學生會求出原函數的能力，以及考查了數形結合的思想，同時會利用定積分求圖形面積的能力，屬于基礎題．