
 .
.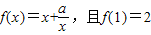 ,可得 1+a=2,解得 a 的值.
,可得 1+a=2,解得 a 的值.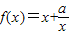 的定義域為{x|x≠1},關于原點對稱,且f(-x)=-f(x),可得函數是奇函數.
的定義域為{x|x≠1},關于原點對稱,且f(-x)=-f(x),可得函數是奇函數.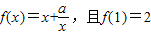 ,∴1+a=2,解得 a=1.
,∴1+a=2,解得 a=1.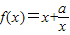 的定義域為{x|x≠1},關于原點對稱,
的定義域為{x|x≠1},關于原點對稱,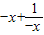 =-(
=-(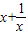 )=-f(x),故函數是奇函數.
)=-f(x),故函數是奇函數.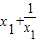 -(
-(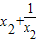 )=(x1-x2)+(
)=(x1-x2)+(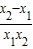 )=(x1-x2) (1-
)=(x1-x2) (1-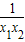 ),
),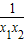 )<0,故有f(x1 )-f(x2)>0,
)<0,故有f(x1 )-f(x2)>0,

 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源:2012-2013學年安徽省合肥市長豐縣雙墩中學高一(上)期末數學試卷(解析版) 題型:解答題
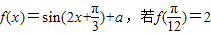 ,
,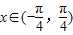 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.查看答案和解析>>
科目:高中數學 來源:2015屆廣東省高一第一次階段考試數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知函數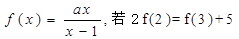 ,
,
(1)求a的值.
(2) 利用單調性定義證明函數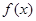 在區間
在區間 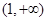 的單調性.
的單調性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com