
 將正奇數列{2n-1}中的所有項按每一行比上一行多一項的規則排成如下數表:
將正奇數列{2n-1}中的所有項按每一行比上一行多一項的規則排成如下數表: (其中x>0),設該數表的第n行的所有數之和為bn,
(其中x>0),設該數表的第n行的所有數之和為bn, .
.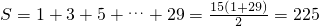 …(3分)
…(3分) 個數,…(7分)
個數,…(7分)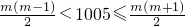 ,
, ,
,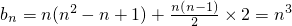 …(12分)
…(12分)
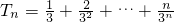 …(1)
…(1)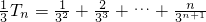 …(2)
…(2) <
<
 .…(14分)
.…(14分) 個數,所以
個數,所以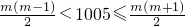 ,由此能求出2009這個數位于第幾行第幾列.
,由此能求出2009這個數位于第幾行第幾列. ,第n行各數形成以n2-n+1為首項,2為公差的等差數列
,第n行各數形成以n2-n+1為首項,2為公差的等差數列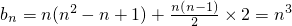 .所以
.所以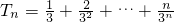 ,再由錯位相減法能夠證明
,再由錯位相減法能夠證明 .
.

科目:高中數學 來源: 題型:
 將正奇數列{2n-1}中的所有項按每一行比上一行多一項的規則排成如下數表:
將正奇數列{2n-1}中的所有項按每一行比上一行多一項的規則排成如下數表:
| |||
| 3n |
| 2009 |
| 2010 |
查看答案和解析>>
科目:高中數學 來源:2009-2010學年山東省日照市六所高中高二(上)期中數學試卷(解析版) 題型:解答題
 (其中x>0),設該數表的第n行的所有數之和為bn,
(其中x>0),設該數表的第n行的所有數之和為bn, .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com