
(Ⅰ)用數(shù)學歸納法證明:當x>-1時,(1+x)m≥1+mx;
(Ⅱ)對于n≥6,已知![]() ,求證
,求證![]() ,m=1,2…,n;
,m=1,2…,n;
(Ⅲ)求出滿足等式3n+4n+…+(n+2)n=(n+3)n的所有正整數(shù)n.
本小題主要考查數(shù)學歸納法、數(shù)列求和,不等式等基礎知識和基本的運算技能,考查分析問題能力和推理能力。
解法1:(Ⅰ)證:用數(shù)學歸納法證明:
(ⅰ)當![]() 時,原不等式成立;當
時,原不等式成立;當![]() 時,左邊
時,左邊![]() ,右邊
,右邊![]() ,
,
因為![]() ,所以左邊
,所以左邊![]() 右邊,原不等式成立;
右邊,原不等式成立;
(ⅱ)假設當![]() 時,不等式成立,即
時,不等式成立,即![]() ,則當
,則當![]() 時,
時,
![]() ,
,![]() ,于是在不等式
,于是在不等式![]() 兩邊同乘以
兩邊同乘以![]() 得
得
![]() ,
,
所以![]() .即當
.即當![]() 時,不等式也成立.
時,不等式也成立.
綜合(ⅰ)(ⅱ)知,對一切正整數(shù)![]() ,不等式都成立.
,不等式都成立.
(Ⅱ)證:當![]() 時,由(Ⅰ)得
時,由(Ⅰ)得![]() ,
,
于是![]()
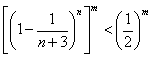 ,
,![]() .
.
(Ⅲ)解:由(Ⅱ)知,當![]() 時,
時,
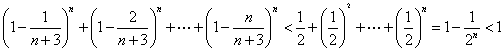 ,
,
![]() .
.
即![]() .即當
.即當![]() 時,不存在滿足該等式的正整數(shù)
時,不存在滿足該等式的正整數(shù)![]() .
.
故只需要討論![]() 的情形:
的情形:
當![]() 時,
時,![]() ,等式不成立;
,等式不成立;
當![]() 時,
時,![]() ,等式成立;
,等式成立;
當![]() 時,
時,![]() ,等式成立;
,等式成立;
當![]() 時,
時,![]() 為偶數(shù),而
為偶數(shù),而![]() 為奇數(shù),故
為奇數(shù),故![]() ,等式不成立;
,等式不成立;
當![]() 時,同
時,同![]() 的情形可分析出,等式不成立.
的情形可分析出,等式不成立.
綜上,所求的![]() 只有
只有![]() .
.
解法2:(Ⅰ)證:當![]() 或
或![]() 時,原不等式中等號顯然成立,下用數(shù)學歸納法證明:
時,原不等式中等號顯然成立,下用數(shù)學歸納法證明:
當![]() ,且
,且![]() 時,
時,![]() ,
,![]() . ①
. ①
(ⅰ)當![]() 時,左邊
時,左邊![]() ,右邊
,右邊![]() ,因為
,因為![]() ,所以
,所以![]() ,即左邊
,即左邊![]() 右邊,不等式①成立;
右邊,不等式①成立;
(ⅱ)假設當![]() 時,不等式①成立,即
時,不等式①成立,即![]() ,則當
,則當![]() 時,
時,
因為![]() ,所以
,所以![]() .又因為
.又因為![]() ,所以
,所以![]() .
.
于是在不等式![]() 兩邊同乘以
兩邊同乘以![]() 得
得
![]() ,
,
所以![]() .即當
.即當![]() 時,不等式①也成立.
時,不等式①也成立.
綜上所述,所證不等式成立.
(Ⅱ)證:當![]() ,
,![]() 時,
時,![]() ,
,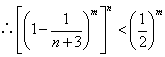 ,
,
而由(Ⅰ),![]() ,
,
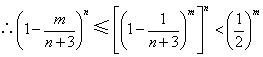 .
.
(Ⅲ)解:假設存在正整數(shù)![]() 使等式
使等式![]() 成立,
成立,
即有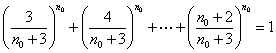 . ②
. ②
又由(Ⅱ)可得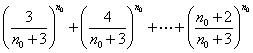
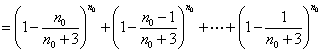
![]() ,與②式矛盾.
,與②式矛盾.
故當![]() 時,不存在滿足該等式的正整數(shù)
時,不存在滿足該等式的正整數(shù)![]() .
.
下同解法1.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
| 1 |
| n+3 |
| 1 |
| 2 |
| m |
| n+3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(湖北理21)(本小題滿分14分)
已知m,n為正整數(shù).
(Ⅰ)用數(shù)學歸納法證明:當x>-1時,(1+x)m≥1+mx;
(Ⅱ)對于n≥6,已知![]() ,求證
,求證![]() ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出滿足等式3n+4m+…+(n+2)m=(n+3)n的所有正整數(shù)n.
查看答案和解析>>
科目:高中數(shù)學 來源:0110 期末題 題型:解答題
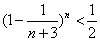 ,求證
,求證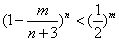 ,m=1,2,3,…,n;
,m=1,2,3,…,n;查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年安徽省蚌埠市懷遠一中高三(下)第六次月考數(shù)學試卷(理科)(解析版) 題型:解答題
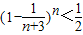 ,求證
,求證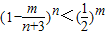 ,m=1,2…,n;
,m=1,2…,n;查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com