
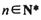 ,總有
,總有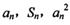 成等差數(shù)列.
成等差數(shù)列.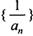 的前n項和為Tn,數(shù)列{Tn}的前n項和為Rn,求證:
的前n項和為Tn,數(shù)列{Tn}的前n項和為Rn,求證: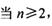
 時,
時,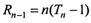 ;
;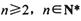 ,試比較
,試比較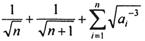 與
與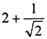 的大小
的大小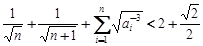
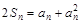 ,遞寫相減得an+1-an=1,由等差數(shù)列求得通項;(II)求出兩邊表達(dá)式證明相等;(III)數(shù)學(xué)歸納法或不等式證明。
,遞寫相減得an+1-an=1,由等差數(shù)列求得通項;(II)求出兩邊表達(dá)式證明相等;(III)數(shù)學(xué)歸納法或不等式證明。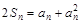 (n∈N*).
(n∈N*).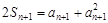 ,
,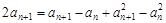 ,
,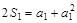 ,得a1=1或a1=0(舍去).
,得a1=1或a1=0(舍去).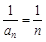 ,于是
,于是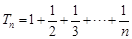 ,
,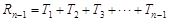 =
=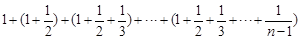
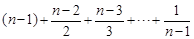
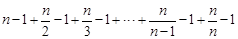
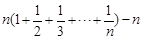 =n(Tn-1). ……………………………10分
=n(Tn-1). ……………………………10分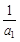 =1,2(T2-1)=2(
=1,2(T2-1)=2(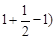 =1,
=1,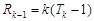 ,
,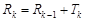
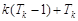 =
= =
=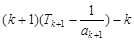
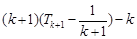 =
=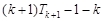 =
=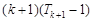 .
.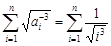 .
.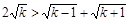 ,
,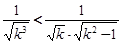
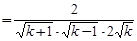

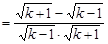
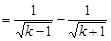 ,∴
,∴ 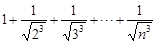
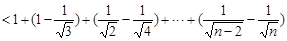
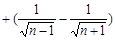
 .即
.即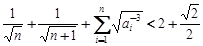 .
.

 全優(yōu)點練單元計劃系列答案
全優(yōu)點練單元計劃系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
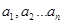 (
(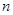 是正整數(shù)),滿足
是正整數(shù)),滿足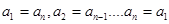 即
即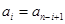 (
(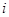 是正整數(shù),且
是正整數(shù),且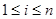 ),就稱該數(shù)列為“對稱數(shù)列”。
),就稱該數(shù)列為“對稱數(shù)列”。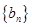 是項數(shù)為7的對稱數(shù)列,且
是項數(shù)為7的對稱數(shù)列,且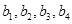 成等差數(shù)列,
成等差數(shù)列,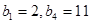 ,試寫出
,試寫出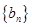 的每一項
的每一項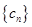 是項數(shù)為
是項數(shù)為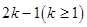 的對稱數(shù)列,且
的對稱數(shù)列,且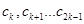 構(gòu)成首項為50,公差為
構(gòu)成首項為50,公差為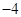 的等差數(shù)列,數(shù)列
的等差數(shù)列,數(shù)列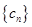 的前
的前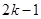 項和為
項和為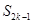 ,則當(dāng)
,則當(dāng)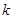 為何值時,
為何值時,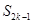 取到最大值?最大值為多少?
取到最大值?最大值為多少?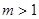 ,試寫出所有項數(shù)不超過
,試寫出所有項數(shù)不超過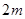 的對稱數(shù)列,使得
的對稱數(shù)列,使得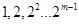 成為數(shù)列中的連續(xù)項;當(dāng)
成為數(shù)列中的連續(xù)項;當(dāng)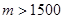 時,試求其中一個數(shù)列的前2008項和
時,試求其中一個數(shù)列的前2008項和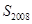
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
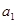 =2,點(
=2,點(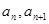 )在函數(shù)
)在函數(shù)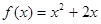 的圖像上,其中
的圖像上,其中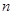 =
=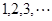 .
.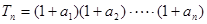 ,求
,求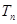 及數(shù)列{
及數(shù)列{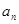 }的通項公式;
}的通項公式;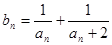 ,求數(shù)列{
,求數(shù)列{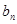 }的前n項和
}的前n項和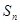 ,并求
,并求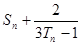 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
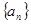 的前
的前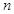 項和為
項和為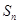 ,若
,若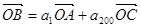 ,且
,且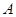 、
、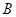 、
、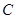 三點共線(該直線不過點
三點共線(該直線不過點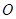 ),則
),則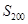 等于( )
等于( )| A.100 | B.200 | C.101 | D.201 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com