Question

已知函數

（I）求的解集；

（II）設a>0,g(x)=ax²－2x＋5, 若對任意實數，均有恒成立，求a的取值范圍。

 

Answer 1

【答案】

（1）t＞2   (2)a≥1

【解析】

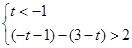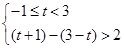試題分析：（I）由函數f（t）=|t+1|-|t-3|＞2可得①，或②，或③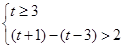．解①得t∈?，解②得 2＜t＜3，解③得 t≥3．綜上可得，不等式的解集為{t|t＞2}．

（II）∵a＞0，g（x）=ax²-2x+5，若對任意實數x、t，均有g（x）≥f（t）恒成立，故有g_min（x）≥f_max（t）．由題意可得，當x=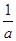時，g（x）取得最小值為g_min（x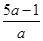）=．而由絕對值的意義可得f（t）的最大值等于4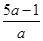，∴≥4，解得 a≥1，故a的取值范圍為[1，+∞）．

考點：本題考查了絕對值不等式的解法、函數的恒成立問題

點評：不等式選講主要考查絕對值不等式的解法、不等式證明及其應用，要求學生學會從分段函數角度來解絕對值不等式及絕對值不等式的最值問題等，掌握常見的證明不等式的方法如綜合法、分析法、數學歸納法等。