
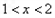 時, f(x)=x+lnx, 求當(dāng)
時, f(x)=x+lnx, 求當(dāng)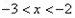 時, f(x)的解析式.
時, f(x)的解析式.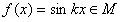 ,求實數(shù)k的取值范圍.
,求實數(shù)k的取值范圍.解: (1) 假設(shè)函數(shù)f(x)=x屬于集合M,
則存在非零常數(shù)T, 對任意x∈R, 有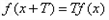 成立,
成立,
即: x+T=Tx成立.
令x=0, 則T=0, 與題矛盾.
故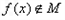 .
.
(2) 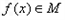 , 且T=2, 則對任意x∈R, 有
, 且T=2, 則對任意x∈R, 有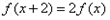 ,
,
設(shè) , 則
, 則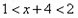 ,
, 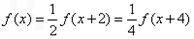
當(dāng)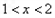 時,
時, 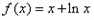 ,
,
故當(dāng)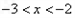 時,
時, 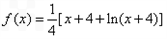 .
.
(3)當(dāng)k=0時,f(x)=0,顯然f(x)=0∈M.
當(dāng)k≠0時,因為f(x)=sinkx∈M,
所以存在非零常數(shù)T,對任意x∈R,有f(x+T)=T f(x)成立,
即sin(kx+kT)=Tsinkx .
因為k≠0,且x∈R,所以kx∈R,kx+kT∈R,
于是sinkx ∈[-1,1],sin(kx+kT) ∈[-1,1],
故要使sin(kx+kT)=Tsinkx .成立,只有T=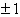 ,
,
①當(dāng)T=1時,sin(kx+k)=sinkx 成立,則k=2mπ, m∈Z .
②當(dāng)T=-1時,sin(kx-k)=-sinkx 成立,即sin(kx-k+π)= sinkx 成立,
則-k+π=2mπ, m∈Z ,即k=-(2m-1)π, m∈Z
綜合得,實數(shù)k的取值范圍是{k|k= nπ, n∈Z}


科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| x |
| a |
| x2+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| k | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| f(x)+λf(t) |
| 1+λ |
| s+λt |
| 1+λ |
| x+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| a |
| 2 |
| b |
| 2 |
| x-1 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com