
��֪�E�A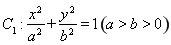 ���x���ʞ�
���x���ʞ�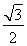 ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n)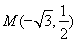 ���A
���A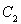 ��ֱ����
��ֱ����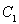 ���L(zh��ng)�S.��D��
���L(zh��ng)�S.��D��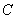 �ǙE�A���S���c(di��n)����(d��ng)ֱ��
�ǙE�A���S���c(di��n)����(d��ng)ֱ��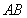 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)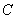 ���c�A
���c�A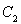 ����
����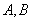 ���c(di��n)��
���c(di��n)��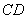 ��ֱ��
��ֱ��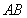 ���E�A���c(di��n)
���E�A���c(di��n) .
.
��1����E�A �ķ��̣�
�ķ��̣�
��2���� ��e�����ֵ������˕r(sh��)ֱ��
��e�����ֵ������˕r(sh��)ֱ��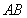 �ķ���.
�ķ���.
��1��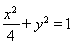 ��2��
��2��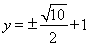
��������
ԇ�}��������1����֪�E�A���x���ʞ�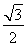 ���ɵõ�
���ɵõ�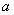 �c
�c ���P(gu��n)ϵʽ
���P(gu��n)ϵʽ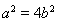 ,�ٽY(ji��)�ϙE�A�^(gu��)�c(di��n)
,�ٽY(ji��)�ϙE�A�^(gu��)�c(di��n)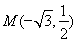 ,����E�A���̽M�ɷ��̽M�����õ��E�A����; ��2�� Ҫ��
,����E�A���̽M�ɷ��̽M�����õ��E�A����; ��2�� Ҫ��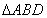 ��e������ɂ�(g��)��
��e������ɂ�(g��)��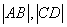 �L(zh��ng)��,
�L(zh��ng)��,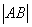 ��һֱ���c�A�ཻ�õ������L(zh��ng),�ɲ��ÈA�����L(zh��ng)��ʽ
��һֱ���c�A�ཻ�õ������L(zh��ng),�ɲ��ÈA�����L(zh��ng)��ʽ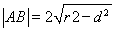 ,��
,��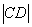 �ǙE�A�����L(zh��ng),ʹ�ù�ʽ
�ǙE�A�����L(zh��ng),ʹ�ù�ʽ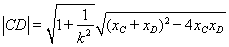 ���,����e��ʾ��׃��
���,����e��ʾ��׃��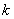 �ĺ���(sh��)
�ĺ���(sh��)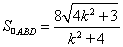 , ������ֵ�r(sh��)���ÓQԪ�����.��(du��)��(d��ng)
, ������ֵ�r(sh��)���ÓQԪ�����.��(du��)��(d��ng) б�ʞ�0�r(sh��)Ҫ�Ϊ�(d��)ӑՓ.
б�ʞ�0�r(sh��)Ҫ�Ϊ�(d��)ӑՓ.
ԇ�}��������1������֪�õ�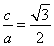 ,����
,����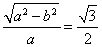 ,��
,��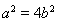 .
.
�֙E�A��(j��ng)�^(gu��)�c(di��n)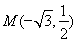 ,��
,��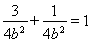 ,
,
���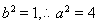 ,
,
���ԙE�A�ķ�����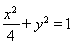
��2����?y��n)�ֱ��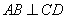 �Ҷ��^(gu��)�c(di��n)
�Ҷ��^(gu��)�c(di��n)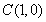
�ٮ�(d��ng)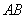 б�ʴ����Ҳ���0�r(sh��),�O(sh��)ֱ��
б�ʴ����Ҳ���0�r(sh��),�O(sh��)ֱ��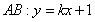 ,ֱ��
,ֱ��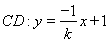 ,��
,��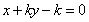 ,
,
���ԈA��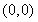 ��ֱ��
��ֱ��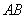 �ľ��x��
�ľ��x��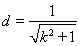 ,����ֱ��
,����ֱ��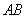 ���A
���A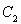 ������
������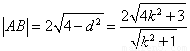
�� ��,
��, 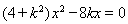
����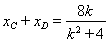
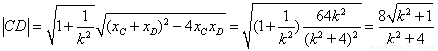 .
.
����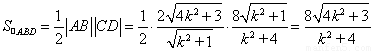 .
.
��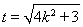 ,�t
,�t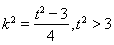 ,
,
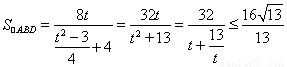
��(d��ng)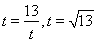 ,��
,��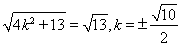 �r(sh��),��̖(h��o)����,
�r(sh��),��̖(h��o)����,
��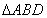 ��e�����ֵ��
��e�����ֵ��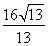 ,�˕r(sh��)ֱ��
,�˕r(sh��)ֱ��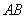 �ķ��̞�
�ķ��̞�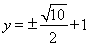
�ڮ�(d��ng) б�ʞ�0�r(sh��),��
б�ʞ�0�r(sh��),��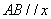 ,�˕r(sh��)
,�˕r(sh��)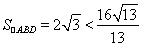
��(d��ng)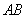 ��б�ʲ����ڕr(sh��),�����}��;
��б�ʲ����ڕr(sh��),�����}��;
�C��, 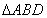 ��e�����ֵ��
��e�����ֵ��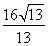 ,�˕r(sh��)ֱ��
,�˕r(sh��)ֱ��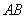 �ķ��̞�
�ķ��̞�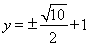 .
.
���c(di��n)��ֱ���c�A��λ���P(gu��n)ϵ,���L(zh��ng)��ʽ,�QԪ����(sh��)��ֵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
A��
| ||||
B��
| ||||
C��
| ||||
| D�����Ͼ�����(du��) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
| 1 |
| 2 |
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
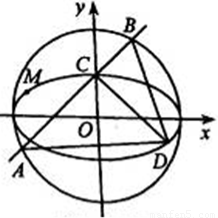
 ��D�����ɈAO��x2+y2=1�͙E�AC��
��D�����ɈAO��x2+y2=1�͙E�AC��| x2 |
| a2 |
| ||
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OM |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
 ��D��A��B�ǙE�AC��
��D��A��B�ǙE�AC��| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com