
一汽車廠生產 、
、 、
、 三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛)
三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛)
| | 轎車 | 轎車 | 轎車 |
| 舒適型 |  |  |  |
| 標準型 |  |  |  |
 輛,其中有
輛,其中有 類轎車
類轎車 輛.
輛. 的值;
的值; 類轎車中抽取一個容量為
類轎車中抽取一個容量為 的樣本.將該樣本看成一個總體,從中任取
的樣本.將該樣本看成一個總體,從中任取 輛,求至少有
輛,求至少有 輛舒適型轎車的概率;
輛舒適型轎車的概率; 類舒適型轎車中抽取
類舒適型轎車中抽取 輛,經檢測它們的得分如下:
輛,經檢測它們的得分如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .把這
.把這 輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值
輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值 的概率.
的概率. (1) ;(2)
;(2)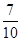 ;(3)
;(3)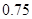 .
.
解析試題分析:(1)先利用分層抽樣的特點求出該公司這個月生產的轎車的總數,然后利用總數減去已知的轎車數求出 的值;(2)利用分層抽樣的特點得出
的值;(2)利用分層抽樣的特點得出 輛轎車中舒適型轎車與標準型轎車的數目,利用列舉法求出相應事件的概率;(3)先求出樣本的平均數,然后確定與平均數之差的絕對值不超過
輛轎車中舒適型轎車與標準型轎車的數目,利用列舉法求出相應事件的概率;(3)先求出樣本的平均數,然后確定與平均數之差的絕對值不超過 的數據,利用古典概型求出相應事件的概率.
的數據,利用古典概型求出相應事件的概率.
試題解析:(1)設該廠本月生產轎車為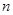 輛,由題意得
輛,由題意得 ,
,
所以 ,
, ;
;
(2)設所抽樣本中有 輛舒適型轎車,因為用分層抽樣,所以
輛舒適型轎車,因為用分層抽樣,所以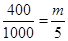 ,解得
,解得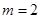 ,
,
即抽取了 輛舒適型轎車,
輛舒適型轎車,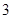 輛標準型轎車,分別記作
輛標準型轎車,分別記作 、
、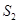 、
、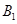 、
、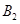 、
、 ,
,
則從中任取 輛的所有基本事件為
輛的所有基本事件為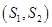 、
、 、
、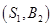 、
、 、
、 、
、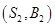 、
、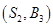 、
、 、
、 、
、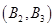 ,共
,共 個,
個,
其中至少有 輛舒適型轎車的基本事件有
輛舒適型轎車的基本事件有 個基本事件:
個基本事件: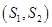 、
、 、
、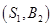 、
、 、
、 、
、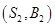 、
、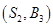 ,
,
所以從中任取 輛,至少有
輛,至少有 輛舒適型轎車的概率為
輛舒適型轎車的概率為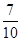 ;
;
(3)樣本的平均數為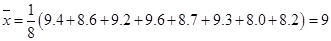 ,
,
那么與樣本平均數之差的絕對值不超過 的數為
的數為 、
、 、
、 、
、 、
、 、
、 這
這 個數,總的個數為
個數,總的個數為 ,
,
所以該數與樣本平均數之差的絕對值不超過 的概率為
的概率為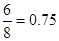 .
.
考點:1.分層抽樣;2.平均數;3.古典概型


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:解答題
(本題滿分12分 )
2013年國慶期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下圖的頻率分布直方圖.
后得到如下圖的頻率分布直方圖.
(1)此調查公司在采樣中,用到的是什么抽樣方法?
(2)求這40輛小型車輛車速的中位數的估計值;
(3)若從車速在 的車輛中任抽取3輛,求抽出的3輛車中車速在
的車輛中任抽取3輛,求抽出的3輛車中車速在 的車輛數
的車輛數 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠生產 、
、 兩種元件,其質量按測試指標劃分為:大于或等于
兩種元件,其質量按測試指標劃分為:大于或等于 為正品,小于
為正品,小于 為次品.現從一批產品中隨機抽取這兩種元件各
為次品.現從一批產品中隨機抽取這兩種元件各 件進行檢測,檢測結果記錄如下:
件進行檢測,檢測結果記錄如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,統計員只記得
看不清,統計員只記得 ,且
,且 、
、 兩種元件的檢測數據的平均值相等,方差也相等.
兩種元件的檢測數據的平均值相等,方差也相等. 與
與 的值;
的值; 件
件 種元件中任取
種元件中任取 件,求
件,求 件都為正品的概率.
件都為正品的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查乘客的候車情況,公交公司在某站臺的60名候車乘客中隨機抽取15人,將他們的候車時間(單位:分鐘)作為樣本分成5組,如下表所示: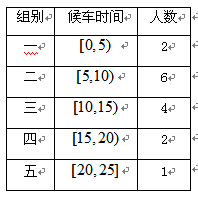
(1)估計這60名乘客中候車時間少于10分鐘的人數;
(2)若從上表第三、四組的6人中隨機抽取2人作進一步的問卷調查,求抽到的兩人恰好來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某居民區隨機抽取10個家庭,獲得第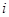 個家庭的月收入
個家庭的月收入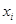 (單位:千元)與月儲蓄
(單位:千元)與月儲蓄 (單位:千元)的數據資料,算得
(單位:千元)的數據資料,算得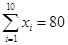 ,
,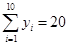 ,
,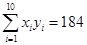 ,
,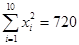 .
.
(1)求家庭的月儲蓄 對月收入
對月收入 的線性回歸方程
的線性回歸方程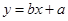 ;
;
(2)判斷變量 與
與 之間是正相關還是負相關;
之間是正相關還是負相關;
(3)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
其中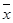 ,
,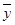 為樣本平均值,線性回歸方程也可寫為
為樣本平均值,線性回歸方程也可寫為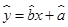
附:線性回歸方程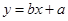 中,
中,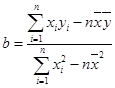 ,
,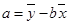 ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某食品廠對生產的某種食品按行業標準分成五個不同等級,等級系數X依次為A,B,C,D,E.現從該種食品中隨機抽取20件樣品進行檢驗,對其等級系數進行統計分析,得到頻率分布表如下:
(1)在所抽取的20件樣品中,等級系數為D的恰有3件,等級系數為E的恰有2件,求a,b,c的值;
(2)在(1)的條件下,將等級系數為D的3件樣品記為x1,x2,x3,等級系數為E的2件樣品記為y1,y2,現從x1,x2,x3,y1,y2這5件樣品中一次性任取兩件(假定每件樣品被取出的可能性相同),試寫出所有可能的結果,并求取出的兩件樣品是同一等級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校隨機抽取部分新生調查其上學路上所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中,上學路上所需時間的范圍是 ,樣本數據分組為
,樣本數據分組為 ,
, ,
, ,
,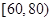 ,
,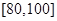 .
.
(1)求直方圖中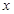 的值;
的值;
(2)如果上學路上所需時間不少于60分鐘的學生可申請在學校住宿,請估計學校1000名新生中有多少名學生可以申請住宿;
(3)現有6名上學路上時間小于 分鐘的新生,其中2人上學路上時間小于
分鐘的新生,其中2人上學路上時間小于 分鐘. 從這6人中任選2人,設這2人中上學路上時間小于
分鐘. 從這6人中任選2人,設這2人中上學路上時間小于 分鐘人數為
分鐘人數為 ,求
,求 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對甲、乙兩名自行車賽手在相同條件下進行了6次測試,測得他們的最大速度(m/s)的數據如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com