
(本小題10分)選修4—1:幾何證明選講
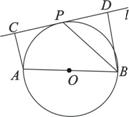
如圖,設(shè)![]() 為⊙O的任一條不與直線l垂直的直徑,
為⊙O的任一條不與直線l垂直的直徑,![]() 是⊙O與l的公共點(diǎn),
是⊙O與l的公共點(diǎn),
![]() ⊥l,
⊥l,![]() ⊥l,垂足分別為
⊥l,垂足分別為![]() ,
,![]() ,且
,且![]() ,求證:
,求證:
(I)l是⊙O的切線;
(II)![]() 平分∠ABD.
平分∠ABD.
|
選修4—1:幾何證明選講
證明:(Ⅰ)連結(jié)OP,因?yàn)锳C⊥l,BD⊥l,
所以AC//BD.
又OA=OB,PC=PD,
所以O(shè)P//BD,從而OP⊥l.
因?yàn)镻在⊙O上,所以l是⊙O的切線. ……………………5分
(Ⅱ)連結(jié)AP,因?yàn)?i>l是⊙O的切線,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.……………………10分
|


 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2011年遼寧省錦州市高三第一學(xué)期末理科數(shù)學(xué)卷 題型:解答題
(本小題10分)選修4—1:幾何證明選講
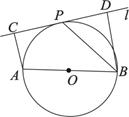
如圖,設(shè)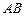 為⊙O的任一條不與直線l垂直的直徑,
為⊙O的任一條不與直線l垂直的直徑,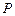 是⊙O與l的公共點(diǎn),
是⊙O與l的公共點(diǎn),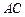 ⊥l,
⊥l,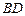 ⊥l,垂足分別為
⊥l,垂足分別為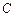 ,
,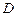 ,且
,且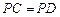 ,
,
求證:
(I)l是⊙O的切線;
(II)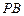 平分∠ABD.
平分∠ABD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013年全國(guó)普通高等學(xué)校招生統(tǒng)一考試?yán)砜茢?shù)學(xué)(新課標(biāo)1卷解析版) 題型:解答題
(本小題10分)選修4—4:坐標(biāo)系與參數(shù)方程
已知曲線C1的參數(shù)方程為 (t為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線C2的極坐標(biāo)方程為ρ=2sinθ。
(t為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線C2的極坐標(biāo)方程為ρ=2sinθ。
(Ⅰ)把C1的參數(shù)方程化為極坐標(biāo)方程;
(Ⅱ)求C1與C2交點(diǎn)的極坐標(biāo)(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013年全國(guó)普通高等學(xué)校招生統(tǒng)一考試文科數(shù)學(xué)(新課標(biāo)1卷解析版) 題型:解答題
(本小題10分)選修4—4:坐標(biāo)系與參數(shù)方程
已知曲線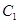 的參數(shù)方程為
的參數(shù)方程為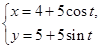 (
(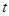 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),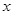 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線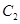 的極坐標(biāo)方程為
的極坐標(biāo)方程為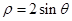 。
。
(Ⅰ)把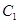 的參數(shù)方程化為極坐標(biāo)方程;
的參數(shù)方程化為極坐標(biāo)方程;
(Ⅱ)求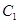 與
與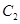 交點(diǎn)的極坐標(biāo)(
交點(diǎn)的極坐標(biāo)(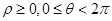 )。
)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
|
已知某圓的極坐標(biāo)方程為![]()
(I)將極坐標(biāo)方程化為普通方程,并選擇恰當(dāng)?shù)膮?shù)寫出它的參數(shù)方程;
(II)若點(diǎn)![]() 在該圓上,求
在該圓上,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com