
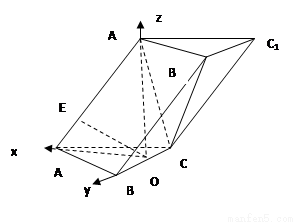
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=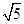 ,BC=4,在A1在底面ABC的投影是線段BC的中點(diǎn)O。
,BC=4,在A1在底面ABC的投影是線段BC的中點(diǎn)O。
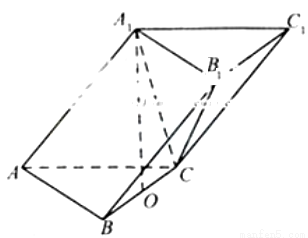
(1)證明在側(cè)棱AA1上存在一點(diǎn)E,使得OE⊥平面BB1C1C,并求出AE的長(zhǎng);
(2)求平面A1B1C與平面BB1C1C夾角的余弦值。
(1)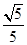 (2)
(2)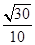
【解析】(1)證明:連接AO,在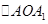 中,作
中,作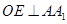 于點(diǎn)E,因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912462104639747/SYS201207091246524526335352_DA.files/image005.png">,得
于點(diǎn)E,因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912462104639747/SYS201207091246524526335352_DA.files/image005.png">,得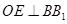 ,
,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912462104639747/SYS201207091246524526335352_DA.files/image007.png">平面ABC,所以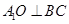 ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912462104639747/SYS201207091246524526335352_DA.files/image009.png">,
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912462104639747/SYS201207091246524526335352_DA.files/image009.png">,
得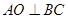 ,所以
,所以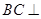 平面
平面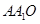 ,所以
,所以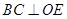 ,
,
所以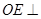 平面
平面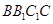 ,又
,又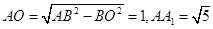 ,得
,得
(2)如圖所示,分別以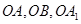 所在的直線為x,y,z軸建立空間直角坐標(biāo)系,則A(1,0,0), C(0,-2,0), A1(0.0,2),B(0,2,0)
所在的直線為x,y,z軸建立空間直角坐標(biāo)系,則A(1,0,0), C(0,-2,0), A1(0.0,2),B(0,2,0)
由(1)可知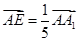 得點(diǎn)E的坐標(biāo)為
得點(diǎn)E的坐標(biāo)為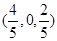 ,由(1)可知平面
,由(1)可知平面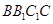 的法向量是
的法向量是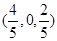 ,設(shè)平面
,設(shè)平面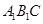 的法向量
的法向量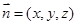 ,
,
由 ,得
,得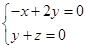 ,令
,令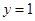 ,得
,得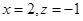 ,即
,即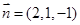
所以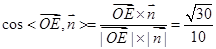
即平面平面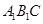 與平面BB1C1C夾角的余弦值是
與平面BB1C1C夾角的余弦值是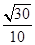 。
。
【點(diǎn)評(píng)】本題考查線面垂直,二面角、向量法在解決立體幾何問(wèn)題中的應(yīng)用以及空間想象的能力. 高考中,立體幾何解答題一般有以下三大方向的考查.一、考查與垂直,平行有關(guān)的線面關(guān)系的證明;二、考查空間幾何體的體積與表面積;三、考查異面角,線面角,二面角等角度問(wèn)題.前兩種考查多出現(xiàn)在第1問(wèn),第3種考查多出現(xiàn)在第2問(wèn);對(duì)于角度問(wèn)題,一般有直接法與空間向量法兩種求解方法.


 通城學(xué)典默寫(xiě)能手系列答案
通城學(xué)典默寫(xiě)能手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
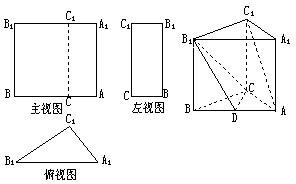 已知三棱柱ABC-A1B1C1的三視圖如圖所示,其中主視圖AA1B1B和左視圖B1BCC1均為矩形,在俯視圖△A1B1C1中,A1C1=3,A1B1=5,cos∠A1=
已知三棱柱ABC-A1B1C1的三視圖如圖所示,其中主視圖AA1B1B和左視圖B1BCC1均為矩形,在俯視圖△A1B1C1中,A1C1=3,A1B1=5,cos∠A1=| 3 | 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖:在正三棱柱ABC-A1 B1 C1中,AB=
如圖:在正三棱柱ABC-A1 B1 C1中,AB=| AA1 | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=| 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=| 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2013•北京)如圖,在三棱柱ABC-A1B1C1中,AA1C1C是邊長(zhǎng)為4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如圖,在三棱柱ABC-A1B1C1中,AA1C1C是邊長(zhǎng)為4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.| BD | BC1 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com