
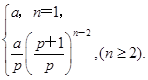 (2)①p=-
(2)①p=-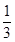 ,dk=9a·2k-1或p=-
,dk=9a·2k-1或p=-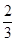 ,dk=
,dk=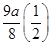 k-1②a=13.
k-1②a=13.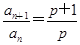 (n≥2),故數列{an}從第二項起是公比為
(n≥2),故數列{an}從第二項起是公比為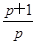 的等比數列,又當n=1時,a1-pa2=0,解得a2=
的等比數列,又當n=1時,a1-pa2=0,解得a2=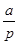 ,
,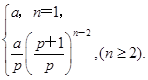
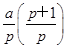 k-1,ak+2=
k-1,ak+2=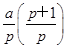 k,ak+3=
k,ak+3=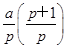 k+1,
k+1,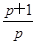 =1或
=1或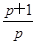 =-2,解得p=-
=-2,解得p=-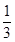 ;
;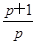 =1,此時無解;
=1,此時無解;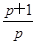 =1或
=1或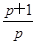 =-
=-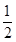 ,
,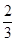 ,
,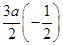 k-1,ak+3=-
k-1,ak+3=-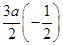 k+1,所以dk=|ak+1-ak+3|=
k+1,所以dk=|ak+1-ak+3|=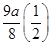 k-1,
k-1,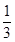 ,dk=9a·2k-1或p=-
,dk=9a·2k-1或p=-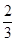 ,dk=
,dk=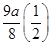 k-1.
k-1.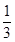 時,Sk=9a(2k-1).
時,Sk=9a(2k-1).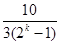 ,
,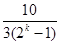 <1,所以必定有a<1,
<1,所以必定有a<1,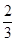 時,Sk=
時,Sk=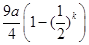 ,
,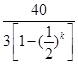 ,因為
,因為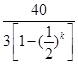 >
>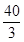 ,所以a=13滿足Sk<30恒成立;但當a=14時,存在k=5,使得a>
,所以a=13滿足Sk<30恒成立;但當a=14時,存在k=5,使得a>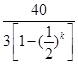 即Sk<30,
即Sk<30,

 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源:不詳 題型:單選題
| A.-100 | B.0 | C.100 | D.200 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
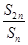 (n∈N*)是非零常數,則稱該數列為“和等比數列”;若數列{cn}是首項為2,公差為d(d≠0)的等差數列,且數列{cn}是“和等比數列”,則d=________.
(n∈N*)是非零常數,則稱該數列為“和等比數列”;若數列{cn}是首項為2,公差為d(d≠0)的等差數列,且數列{cn}是“和等比數列”,則d=________.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com