
已知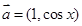 ,
,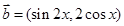 ,且
,且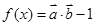
(1)求函數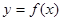
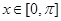 的單調增區間;
的單調增區間;
(2)三角形ABC中,邊 分別為角
分別為角 的對邊,若
的對邊,若 ,B=
,B=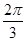 ,且
,且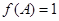 , 求三角形ABC的邊
, 求三角形ABC的邊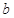 的值.
的值.
(1)單調增區間為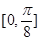 和
和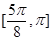 ;(2)
;(2)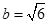 .
.
解析試題分析:(1)首先由向量的數量積及坐標運算得函數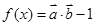 的解析式,利用正弦函數的單調區間即可求得該函數的單調區間;(2)注意直線
的解析式,利用正弦函數的單調區間即可求得該函數的單調區間;(2)注意直線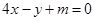 的斜率為4,那么要證明無論
的斜率為4,那么要證明無論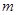 為何值,直線
為何值,直線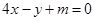 與函數
與函數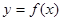 的圖象不相切,就只需通過求導說明函數的導數值不可能等于4即可.
的圖象不相切,就只需通過求導說明函數的導數值不可能等于4即可.
(2)由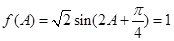 可求得角A.這樣本題就是典型的已知兩角及一邊的解三角形問題,用正弦定理即可求得
可求得角A.這樣本題就是典型的已知兩角及一邊的解三角形問題,用正弦定理即可求得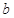 的值.
的值.
試題解析:(1)∵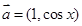 ,
,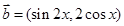 ,且
,且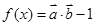
∴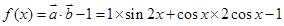 1分
1分
=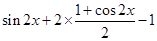 =
=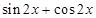
=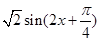 3分
3分
令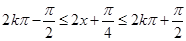 ,解之得
,解之得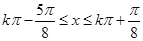 4分
4分
又∵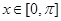 ∴
∴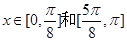
故函數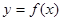
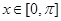 的單調增區間為
的單調增區間為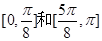 6分
6分
(2)由①問可知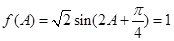
∴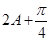 =
=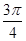 或
或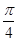 ,即
,即 或
或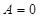 8分
8分
∵A是三角形ABC的內角 ∴
又∵ ,B=
,B=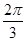 ∴由正弦定理有
∴由正弦定理有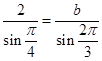 ,即有
,即有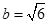 12分
12分
考點:1、向量的數量積及坐標運算;2、三角變換及三角函數的單調區間;3、解三角形.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com