
(本題12分) 某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶的碳月排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少
某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶的碳月排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少 的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .若備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .若備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
(1)求所選的兩個小區恰有一個為“非低碳小區”的概率;
(2)假定選擇的“非低碳小區”為小區 ,調查顯示其“低碳族”的比例為1:2,數據如圖1所示,經過大力宣傳,三個月后又進行一次調查,數據如圖2所示,問這時小區
,調查顯示其“低碳族”的比例為1:2,數據如圖1所示,經過大力宣傳,三個月后又進行一次調查,數據如圖2所示,問這時小區 是否達到“低碳小區”的標準?
是否達到“低碳小區”的標準?
(1)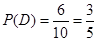 . (2)三個月后小區
. (2)三個月后小區 達到了“低碳小區”標準.
達到了“低碳小區”標準.
解析試題分析:(1)設三個“非低碳小區”為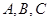 ,兩個“低碳小區”為
,兩個“低碳小區”為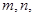 …………1分
…………1分
用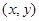 表示選定的兩個小區,
表示選定的兩個小區,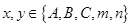 ,
,
則從5個小區中任選兩個小區,所有可能的結果有10個: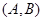 ,
,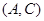 ,
,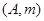 ,
,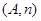 ,
,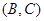 ,
, ,
,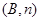 ,
,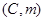 ,
,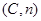 ,
,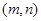 . …………4分
. …………4分
用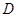 表示:“選出的兩個小區恰有一個為非低碳小區”這一事件,則
表示:“選出的兩個小區恰有一個為非低碳小區”這一事件,則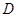 中的結果有6個:
中的結果有6個: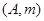 ,
,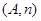 ,
, ,
,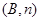 ,
,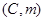 ,
,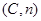 .……6分 故所求概率為
.……6分 故所求概率為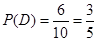 .……7分
.……7分
(2)由圖1可知月碳排放量不超過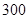 千克的成為“低碳族”. …………9分
千克的成為“低碳族”. …………9分
由圖2可知,三個月后的低碳族的比例為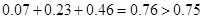 ,……11分
,……11分
所以三個月后小區 達到了“低碳小區”標準. …………12分
達到了“低碳小區”標準. …………12分
考點:本題主要考查古典概型的概率計算;頻率分布直方圖;用樣本的頻率分布估計總體分布。
點評:基礎題,利用列舉法計算基本事件數及事件發生事件數,是古典概型概率計算中的常見題型。


科目:高中數學 來源: 題型:解答題
2012年3月2日,國家環保部發布了新修訂的《環境空氣質量標準》.其中規定:居民區中的PM2.5(PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱可入肺顆粒物)年平均濃度不得超過35微克/立方米,PM2.5的24小時平均濃度不得超過75微克/立方米. 某城市環保部門隨機抽取了一居民區去年40天的PM2.5的24小時平均濃度的監測數據,數據統計如下:
| 組別 | PM2.5(微克/立方米) | 頻數(天) | 頻率 |
| 第一組 | (0,15] | 4 | 0.1 |
| 第二組 | (15,30] | 12 | 0.3 |
| 第三組 | (30,45] | 8 | 0.2 |
| 第四組 | (45,60] | 8 | 0.2 |
| 第三組 | (60,75] | 4 | 0.1 |
| 第四組 | (75,90) | 4 | 0.1 |
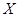 ,求
,求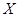 的分布列及數學期望
的分布列及數學期望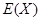 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
甲、乙兩臺機床生產同一型號零件.記生產的零件的尺寸為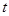 (cm),相關行業質檢部門規定:若
(cm),相關行業質檢部門規定:若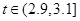 ,則該零件為優等品;若
,則該零件為優等品;若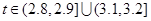 ,則該零件為中等品;其余零件為次品.現分別從甲、乙機床生產的零件中各隨機抽取50件,經質量檢測得到下表數據:
,則該零件為中等品;其余零件為次品.現分別從甲、乙機床生產的零件中各隨機抽取50件,經質量檢測得到下表數據:
| 尺寸 | 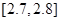 | 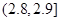 | 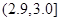 | 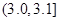 | 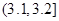 | 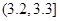 |
| 甲機床零件頻數 | 2 | 3 | 20 | 20 | 4 | 1 |
| 乙機床零件頻數 | 3 | 5 | 17 | 13 | 8 | 4 |
 .
.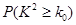 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
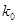 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題10分)某化肥廠甲、乙兩個車間包裝肥料,在自動包裝傳送帶上每隔30min抽取一包產品,稱其重量,分別記錄抽查數據如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)這種抽樣方法是哪一種?
(Ⅱ)將這兩組數據用莖葉圖表示出來;
(Ⅲ)將兩組數據比較:說明哪個車間的產品較穩定。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了了解中學生的體能情況,抽取了某中學同年級部分學生進行跳繩測試,將所得的數據整理后畫出頻率分布直方圖(如下圖),已知圖中從左到右的前三個小組的頻率分別是0.1,0.3,0.4.第一小組的頻數是5.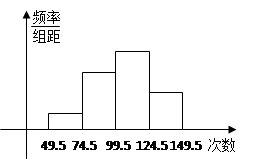
(1) 求第四小組的頻率和參加這次測試的學生人數;
(2) 在這次測試中,學生跳繩次數的中位數落在第幾小組內?
(3) 參加這次測試跳繩次數在100次以上為優秀,試估計該校此年級跳繩成績的優秀率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)一個質地均勻的正四面體的四個面上分別標示著數字1、2、3、4,一個質地均勻的骰子(正方體)的六個面上分別標示數字1、2、3、4、5、6,先后拋擲一次正四面體和骰子。
⑴列舉出全部基本事件;
⑵求被壓在底部的兩個數字之和小于5的概率;
⑶求正四面體上被壓住的數字不小于骰子上被壓住的數字的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
2012年3月2日,國家環保部發布了新修訂的《環境空氣質量標準》.其中規定:居民區中的PM2.5(PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱可入肺顆粒物)年平均濃度不得超過35微克/立方米,PM2.5的24小時平均濃度不得超過75微克/立方米. 某城市環保部門隨機抽取了一居民區去年40天的PM2.5的24小時平均濃度的監測數據,數據統計如下:
| 組別 | PM2.5(微克/立方米) | 頻數(天) | 頻率 |
| 第一組 | (0,15] | 4 | 0.1 |
| 第二組 | (15,30] | 12 | 0.3 |
| 第三組 | (30,45] | 8 | 0.2 |
| 第四組 | (45,60] | 8 | 0.2 |
| 第三組 | (60,75] | 4 | 0.1 |
| 第四組 | (75,90) | 4 | 0.1 |
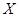 ,求
,求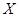 的分布列及數學期望
的分布列及數學期望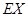 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)為了了解某年段1000名學生的百米成績情況,隨機抽取了若干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.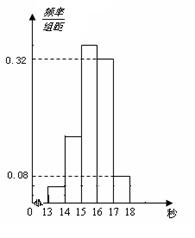
⑴將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
⑵求調查中隨機抽取了多少個學生的百米成績;
⑶若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩位學生參加數學競賽培訓.現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次.記錄如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)畫出甲、乙兩位學生成績的莖葉圖,指出學生乙成績的中位數;
(2)現要從中選派一人參加數學競賽,從平均狀況和方差的角度考慮,你認為派哪位學生參加合適?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com