
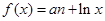 ,其中實數a為常數.
,其中實數a為常數.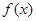 的單調區間:
的單調區間: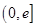 (e為自然對數的底數)上的最大值為-3,求a的值;
(e為自然對數的底數)上的最大值為-3,求a的值;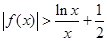 .
.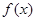 在區間
在區間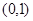 上為增函數,在區間
上為增函數,在區間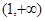 上為減函數.(Ⅱ)
上為減函數.(Ⅱ)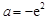 . (Ⅲ) 見解析.
. (Ⅲ) 見解析.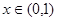 時,
時,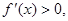
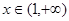 時,
時,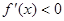 ,單調函數的單調區間.
,單調函數的單調區間.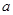 的方程.注意分①
的方程.注意分①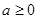 ;②
;②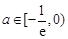 ;③
;③ ,等不同情況加以討論.
,等不同情況加以討論.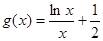 ,利用“導數法”,研究
,利用“導數法”,研究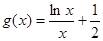 有最大值
有最大值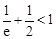 ,根據
,根據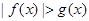 , 得證.
, 得證.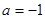 時,
時,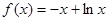 ,∴
,∴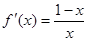 ,又
,又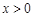 ,所以
,所以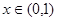 時,
時,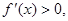
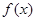 在區間
在區間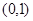 上為增函數,
上為增函數,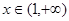 時,
時,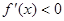 ,
,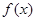 在區間
在區間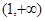 上為減函數,
上為減函數,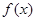 在區間
在區間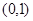 上為增函數,在區間
上為增函數,在區間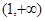 上為減函數. 4分
上為減函數. 4分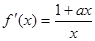 ,①若
,①若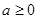 ,∵
,∵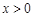 ,則
,則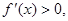 在區間
在區間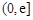 上恒成立,
上恒成立,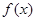 在區間
在區間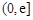 上為增函數,
上為增函數,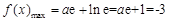 ,∴
,∴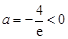 ,舍去;
,舍去;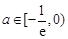 時,∵
時,∵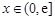 ,∴
,∴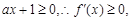
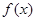 在區間
在區間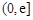 上為增函數,
上為增函數,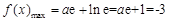 ,∴
,∴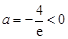 ,舍去;
,舍去; ,當
,當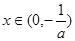 時,
時,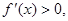
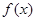 在區間
在區間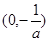 上為增函數,
上為增函數,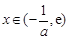 時,
時, 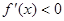 ,
,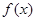 在區間
在區間 上為減函數,
上為減函數,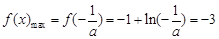 ,∴
,∴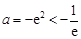 .
.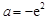 . 9分
. 9分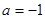 時,
時,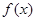 有最大值,最大值為
有最大值,最大值為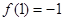 ,即
,即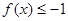 ,
,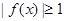 , 10分
, 10分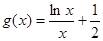 ,則
,則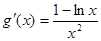 ,
,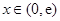 時,
時,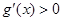 ,
,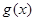 在區間
在區間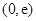 上為增函數,
上為增函數,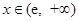 時,
時,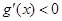 ,
,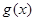 在區間
在區間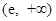 上為減函數,
上為減函數,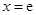 時,
時,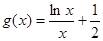 有最大值
有最大值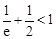 ,12分
,12分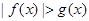 ,
, 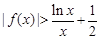 . 13分
. 13分

 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:高中數學 來源:不詳 題型:解答題
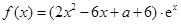 (
(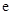 為自然對數的底數).
為自然對數的底數).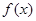 在
在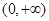 上的單調區間;
上的單調區間;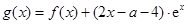 ,是否存在區間
,是否存在區間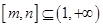 ,使得當
,使得當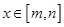 時函數
時函數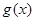 的值域為
的值域為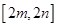 ,若存在求出
,若存在求出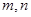 ,若不存在說明理由.
,若不存在說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
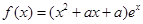 (
(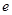 為自然對數的底數)。
為自然對數的底數)。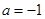 ,求函數
,求函數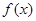 的單調區間;
的單調區間;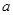 ,使函數
,使函數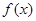 在
在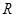 上是單調增函數?若存在,求出
上是單調增函數?若存在,求出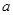 的值;若不存在,請說明理由。恒成立,則
的值;若不存在,請說明理由。恒成立,則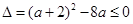
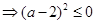 ,又
,又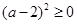 ,
,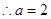
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
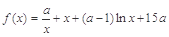 ,
,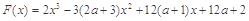 ,其中
,其中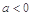 且
且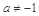 .
. 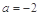 ,求函數
,求函數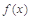 的單調遞增區間;
的單調遞增區間;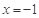 時,函數
時,函數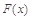 有極值,求函數
有極值,求函數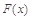 圖象的對稱中心的坐標;
圖象的對稱中心的坐標;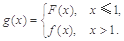 (
(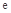 是自然對數的底數),是否存在a使
是自然對數的底數),是否存在a使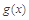 在
在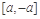 上為減函數,若存在,求實數a的范圍;若不存在,請說明理由.
上為減函數,若存在,求實數a的范圍;若不存在,請說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com