
| 家電名稱 | 空調器 | 彩電 | 冰箱 |
| 工時 |  |  |  |
| 產值(千元) | 4 | 3 | 2 |
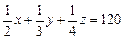 ②
②

 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 .
.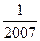 )+f(-
)+f(-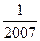 )的值;
)的值; 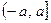 (其中a∈(0, 1), 且a為常數)時,
(其中a∈(0, 1), 且a為常數)時, 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
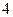 月份,有一新款服裝投入某商場銷售,
月份,有一新款服裝投入某商場銷售,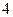 月
月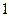 日該款服裝僅銷售出
日該款服裝僅銷售出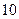 件,第二天售出
件,第二天售出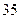 件,第三天銷售
件,第三天銷售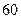 件,然后,每天售出的件數分別遞增
件,然后,每天售出的件數分別遞增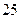 件,直到日銷售量達到最大后,每天銷售的件數分別遞減
件,直到日銷售量達到最大后,每天銷售的件數分別遞減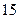 件,到月底該服裝共銷售出
件,到月底該服裝共銷售出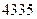 件.(Ⅰ)問
件.(Ⅰ)問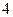 月幾號該款服裝銷售件數最多?其最大值是多少?(Ⅱ)按規律,當該商場銷售此服裝超過
月幾號該款服裝銷售件數最多?其最大值是多少?(Ⅱ)按規律,當該商場銷售此服裝超過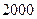 件時,社會上就流行,而日銷售量連續下降,并低于
件時,社會上就流行,而日銷售量連續下降,并低于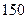 件時,則流行消失,問該款服裝在社會上流行是否超過
件時,則流行消失,問該款服裝在社會上流行是否超過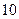 天?并說明理由。
天?并說明理由。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
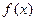 是定義域為[-3,3]的函數,并且設
是定義域為[-3,3]的函數,并且設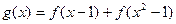 ,
,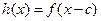 ,其中常數c為實數.(1)求
,其中常數c為實數.(1)求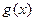 和
和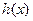 的定義域;(2)如果
的定義域;(2)如果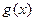 和
和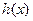 兩個函數的定義域的交集為非空集合,求c的取值范圍;(3)當
兩個函數的定義域的交集為非空集合,求c的取值范圍;(3)當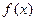 在其定義域內是奇函數,又是增函數時,求使
在其定義域內是奇函數,又是增函數時,求使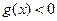 的自變量
的自變量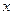 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com