(本題滿分12分)
已知橢圓

的離心率為
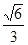
,橢圓C上任意一點到橢圓兩個焦點的距離之和為6。
(1)求橢圓C的方程;
(2)設(shè)直線
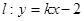
與橢圓C交于A、B兩點,點P(0,1),且|PA|=|PB|,求直線
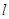
的方程。
(1)
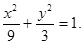
(2)
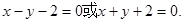
試題分析:解:(I)由已知

,解得

所以橢圓C的方程為
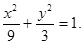
(2)由

,
直線與橢圓有兩個不同的交點,所以
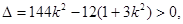
解得

設(shè)
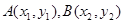
,
則
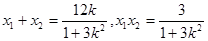
計算
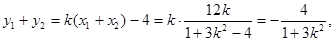
所以,A,B中點坐標(biāo)為
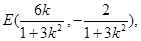
因為|PA|=|PB|,所以PE⊥AB,
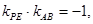
所以
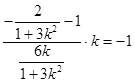
,解得
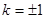
,經(jīng)檢驗,符合題意,
所以直線l的方程為
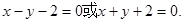
點評:當(dāng)一道題出現(xiàn)什么樣的曲線時,它有什么特點要先明確,一般在解題過程中都可能用到,像本題第一小題用到橢圓的特點:橢圓上任何一點到兩焦點的距離之和等于2a。第二題關(guān)鍵要轉(zhuǎn)換|PA|=|PB|為PE⊥AB(E為A、B的中點)。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
拋物線y
2=2Px,過點A(2,4),F(xiàn)為焦點,定點B的坐標(biāo)為(8,-8),則|AF|∶|BF|值為
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知雙曲線
C 2
x2-
y2=2與點
P(1,2)
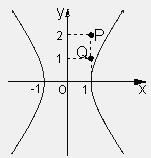
(1)求過
P(1,2)點的直線
l的斜率取值范圍,使
l與
C分別有一個交點,兩個交點,沒有交點
(2)若
Q(1,1),試判斷以
Q為中點的弦是否存在
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知P為拋物線
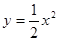
上的動點,點P在x軸上的射影為M,點A的坐標(biāo)是
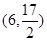
,則
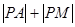
的最小值是( )
| A.8 | B.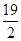 | C.10 | D.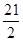 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知直線
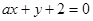
與雙曲線

的一條漸近線平行,則這兩條平行直線之間的距離是
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)A、B為在雙曲線
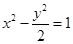
上兩點,O為坐標(biāo)原點.若
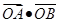
=0,則ΔAOB面積的最小值為______
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
雙曲線
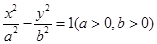
的漸近線都與圓
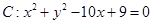
相切,且雙曲線的右焦點為圓C的圓心,則該雙曲線的方程是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
方程2
x2+
ky2=1表示的是焦點在
y軸上的橢圓,則實數(shù)
k的取值范圍是( )
| A.(0,+∞) | B.(2,+∞) | C.(0,2) | D.(0,1) |
查看答案和解析>>

 的離心率為
的離心率為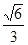 ,橢圓C上任意一點到橢圓兩個焦點的距離之和為6。
,橢圓C上任意一點到橢圓兩個焦點的距離之和為6。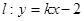 與橢圓C交于A、B兩點,點P(0,1),且|PA|=|PB|,求直線
與橢圓C交于A、B兩點,點P(0,1),且|PA|=|PB|,求直線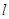 的方程。
的方程。 同步輕松練習(xí)系列答案
同步輕松練習(xí)系列答案 課課通課程標(biāo)準(zhǔn)思維方法與能力訓(xùn)練系列答案
課課通課程標(biāo)準(zhǔn)思維方法與能力訓(xùn)練系列答案