
解:設(shè)月生產(chǎn)產(chǎn)品X、Y分別為x件、y件,該月產(chǎn)品利潤為z,
則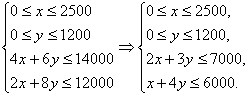
目標(biāo)函數(shù)z=1 000x+2 000y,即z=1 000(x+2y).
設(shè)x+2y=λ(2x+3y)+k(x+4y),易得λ=![]() ,k=
,k=![]() .
.
∴x+2y=![]() (2x+3y)+
(2x+3y)+![]() (x+4y)≤
(x+4y)≤![]() ×7 000+
×7 000+![]() ×6 000=4 000.
×6 000=4 000.
∴zmax=1 000×4 000=4 000 000元=400(萬元).
等號(hào)成立的條件是![]() 即
即![]()
故組裝X產(chǎn)品2 000件,Y產(chǎn)品1 000件時(shí),月利潤最高,最高利潤為400萬元.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
某廠使用兩種零件A、B裝配兩種產(chǎn)品P、Q,該廠的生產(chǎn)能力是月產(chǎn)P產(chǎn)品最多有2500件,月產(chǎn)Q產(chǎn)品最多有1200件;而且組裝一件P產(chǎn)品要4個(gè)A、2個(gè)B,組裝一件Q產(chǎn)品要6個(gè)A、8個(gè)B,該廠在某個(gè)月能用的A零件最多14000個(gè);B零件最多12000個(gè). 已知P產(chǎn)品每件利潤1000元,Q產(chǎn)品每件2000元,欲使月利潤最大,需要組裝P、Q產(chǎn)品各多少件?最大利潤多少萬元.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年湖南省益陽市箴言中學(xué)模塊數(shù)學(xué)試卷(必修5)(解析版) 題型:解答題
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com