
(本小題滿分12分)
已知函數 是奇函數:
是奇函數:
(1)求實數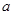 和
和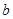 的值;
的值;
(2)證明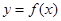 在區間
在區間 上的單調遞減
上的單調遞減
(3)已知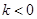 且不等式
且不等式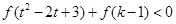 對任意的
對任意的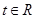 恒成立,求實數
恒成立,求實數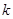 的取值范圍.
的取值范圍.
(1)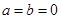 ;(2)見解析;(3)
;(2)見解析;(3)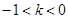 .
.
解析試題分析:(Ⅰ)先根據f(1)=f(4)求出b的值;再結合f(x)+f(-x)=0對x≠0恒成立求出a的值即可;
(Ⅱ)直接按照單調性的證明過程來證即可;
(Ⅲ)先結合第二問的結論知道函數f(x)在(1,+∞)上遞減,進而得到函數的不等式,最后把兩個成立的范圍相結合即可求出結論.
(1)由定義易得: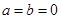
(2)設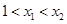 ,
,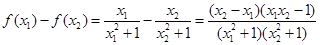
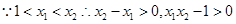 即
即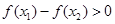 所以
所以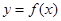 在
在 上的單調遞減。
上的單調遞減。
(3)已知 且不等式
且不等式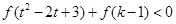 對任意的
對任意的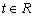 恒成立,求實數
恒成立,求實數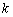 的取值范圍.
的取值范圍.
由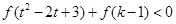 及
及 為奇函數得:
為奇函數得: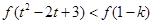
因為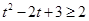 ,
,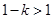 ,且
,且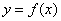 在區間
在區間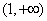 上的單調遞減,
上的單調遞減,
故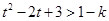 任意的
任意的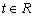 恒成立,故
恒成立,故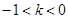 .
.
考點:本題主要是考查函數奇偶性與單調性的綜合.
點評:解決第一問的關鍵在于利用奇函數的定義得到f(x)+f(-x)=0對x≠0恒成立求出a的值.


科目:高中數學 來源: 題型:解答題
(滿分12分)
某市居民生活用水標準如下:
| 用水量t(單位:噸) | 每噸收費標準(單位:元) |
| 不超過2噸部分 | m |
| 超過2噸不超過4噸部分 | 3 |
| 超過4噸部分 | n |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)某市“環保提案”對某處的環境狀況進行了實地調研,據測定,該處的污染指數與附近污染源的強度成正比,與到污染源的距離成反比,比例常數為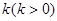 .現已知相距
.現已知相距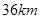 的
的 ,
, 兩家化工廠(污染源)的污染強度分別為正數
兩家化工廠(污染源)的污染強度分別為正數 ,
, ,它們連線上任意一點C處的污染指數
,它們連線上任意一點C處的污染指數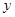 等于兩化工廠對該處的污染指數之和.設
等于兩化工廠對該處的污染指數之和.設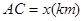 .
.
(1) 試將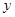 表示為
表示為 的函數;
的函數;
(2) 若 時,
時,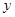 在
在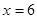 處取得最小值,試求
處取得最小值,試求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分15分)將進貨單價為80元的商品按90元一個售出時,能賣出400個,已知這種商品每個漲價1元,其銷售量就減少10個,為了取得最大利潤,每個售價應定為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12)
為了綠化城市,準備在如圖所示的區域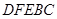 內修建一個矩形
內修建一個矩形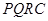 的草坪,并建立如圖平面直角坐標系,且
的草坪,并建立如圖平面直角坐標系,且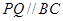 ,
,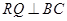 ,另外
,另外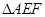 的內部有一文物保護區不能占用,經測量
的內部有一文物保護區不能占用,經測量 ,
,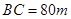 ,
, 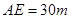 ,
,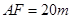 .
.
(1)求直線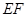 的方程;
的方程;
(2)應如何設計才能使草坪的占地面積最大?并求最大面積。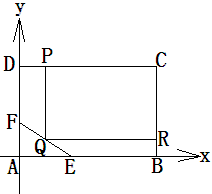
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分) 已知函數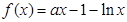
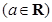 .
.
(1)討論函數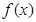 在定義域內的極值點的個數;
在定義域內的極值點的個數;
(2)若函數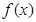 在
在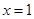 處取得極值,對
處取得極值,對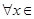
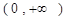 ,
,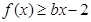 恒成立,求實數
恒成立,求實數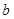 的取值范圍;
的取值范圍;
(3)當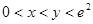 且
且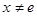 時,試比較
時,試比較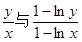 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數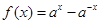 ,
,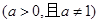 ,
,
(1) 判斷函數 的奇偶性,并證明;
的奇偶性,并證明;
(2) 判斷 的單調性,并說明理由。(不需要嚴格的定義證明,只要說出理由即可)
的單調性,并說明理由。(不需要嚴格的定義證明,只要說出理由即可)
(3) 若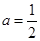 ,方程
,方程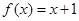 是否有根?如果有根
是否有根?如果有根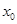 ,請求出一個長度為1的區間
,請求出一個長度為1的區間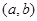 ,使
,使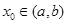 ;如果沒有,請說明理由。(注:區間
;如果沒有,請說明理由。(注:區間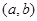 的長度=
的長度=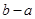 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com