
甲、乙兩地相距1000 ,貨車從甲地勻速行駛到乙地,速度不得超過80
,貨車從甲地勻速行駛到乙地,速度不得超過80 ,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的
,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的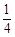 倍,固定成本為a元.
倍,固定成本為a元.
(1)將全程運輸成本y(元)表示為速度v( )的函數,并指出這個函數的定義域;
)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,貨車應以多大的速度行駛?
(1)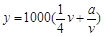 ,
,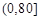 (2)當
(2)當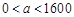 (元)時,
(元)時,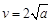 ;當
;當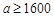 (元)時,
(元)時,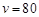 .
.
解析試題分析:(1)解決應用題問題首先要解決閱讀問題,具體說就是要會用數學式子正確表示數量關系,本題中全程運輸成本等于每小時運輸成本與全程所化時間的乘積,有學生錯誤將每小時運輸成本理解為全程運輸成本,其次要注意定義域的確定,不僅要從保證數學式子的有意義考慮,而且更要結合實際意義考慮,如本題速度為正數,(2)研究對應解析式的最值問題,一般從不等式或函數考慮,從不等式考慮時,要會將解析式轉為“和”與“積”的關系,注意等于號是否取到,而從函數考慮時,經常結合導數進行研究.本題不管從不等式考慮還是從函數考慮,都需進行討論,討論的原因都是因為定義域.
試題解析:(1)可變成本為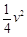 ,固定成本為
,固定成本為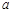 元,所用時間為
元,所用時間為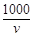 .
.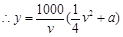 ,即
,即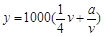 4分
4分
定義域為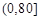 5分
5分
(2)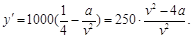
令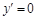 得
得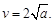 7分
7分
因為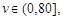
所以當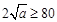 即
即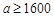 時
時 ,
,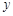 為
為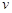 的減函數,
的減函數,
在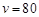 時,
時,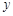 最小. 9分
最小. 9分
所以當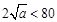 ,即
,即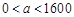 時,
時,
在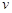
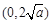
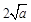
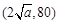
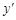
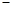

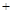
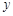
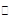
極小值 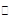
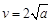 時,
時,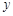 最小. 13分
最小. 13分
(答)以上說明,當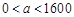 (元)時,貨車以
(元)時,貨車以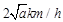 的速度行駛,全程運輸成本最小;當
的速度行駛,全程運輸成本最小;當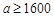 (元)時,貨車以
(元)時,貨車以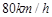 的速度行駛,全程運輸成本最小. 14分
的速度行駛,全程運輸成本最小. 14分
考點:函數解析式,利用導數求函數最值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
(2013·重慶卷)設f(x)=a(x-5)2+6ln x,其中a∈R,曲線y=f(x)在點(1,f(1))處的切線與y軸相交于點(0,6).
(1)確定a的值;
(2)求函數f(x)的單調區間與極值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數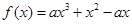 ,其中
,其中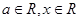 .
.
(1)當 時,求函數
時,求函數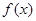 在
在 處的切線方程;
處的切線方程;
(2)若函數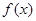 在區間(1,2)上不是單調函數,試求
在區間(1,2)上不是單調函數,試求 的取值范圍;
的取值范圍;
(3)已知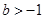 ,如果存在
,如果存在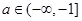 ,使得函數
,使得函數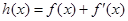
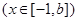 在
在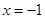 處取得最小值,試求
處取得最小值,試求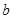 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數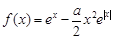 .
.
(Ⅰ)若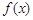 是
是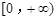 上是增函數,求實數a的取值范圍;
上是增函數,求實數a的取值范圍;
(Ⅱ)證明:當a≥1時,證明不等式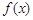 ≤x+1對x∈R恒成立;
≤x+1對x∈R恒成立;
(Ⅲ)對于在(0,1)中的任一個常數a,試探究是否存在x0>0,使得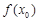 >x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
>x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,
, .
.
(1)若 ,則
,則 ,
, 滿足什么條件時,曲線
滿足什么條件時,曲線 與
與 在
在 處總有相同的切線?
處總有相同的切線?
(2)當 時,求函數
時,求函數 的單調減區間;
的單調減區間;
(3)當 時,若
時,若 對任意的
對任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,
, ,
, ,其中
,其中 ,且
,且 .
.
⑴當 時,求函數
時,求函數 的最大值;
的最大值;
⑵求函數 的單調區間;
的單調區間;
⑶設函數 若對任意給定的非零實數
若對任意給定的非零實數 ,存在非零實數
,存在非零實數 (
( ),使得
),使得 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com