
 .
. ,求
,求 的極值;
的極值; 在定義域內無極值,求實數
在定義域內無極值,求實數 的取值范圍.
的取值范圍.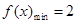 ,
,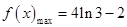 ;(Ⅱ)
;(Ⅱ) 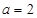 .
. 時的函數解析式以及定義域:
時的函數解析式以及定義域: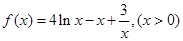 ,對函數求導并且求得函數的零點,結合導數的正負判斷函數在零點所分的各個區間上的單調性,從而得到函數的極值點,求得極值點對應的函數值即可;(Ⅱ)先求出函數
,對函數求導并且求得函數的零點,結合導數的正負判斷函數在零點所分的各個區間上的單調性,從而得到函數的極值點,求得極值點對應的函數值即可;(Ⅱ)先求出函數 的導數,將問題“
的導數,將問題“ 在定義域內無極值”轉化為“
在定義域內無極值”轉化為“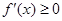 或
或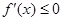 在定義域上恒成立”,那么設
在定義域上恒成立”,那么設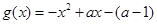 分兩種情況進行討論,分別為方程無解時
分兩種情況進行討論,分別為方程無解時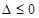 ,以及方程有解時保證
,以及方程有解時保證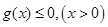 ,即
,即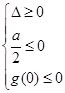 成立,解不等式及不等式組,求兩種情況下解的并集.
成立,解不等式及不等式組,求兩種情況下解的并集. ,∴
,∴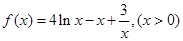 , 1分
, 1分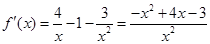 , 2分
, 2分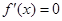 ,解得
,解得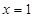 或
或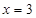 . 3分
. 3分 時,
時,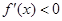 ;
;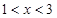 時,
時,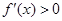 . 4分
. 4分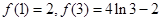 , 5分
, 5分 取得極小值2,極大值
取得極小值2,極大值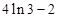 . 6分
. 6分 ,
, , 7分
, 7分 在定義域內無極值,即
在定義域內無極值,即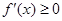 或
或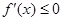 在定義域上恒成立. 9分
在定義域上恒成立. 9分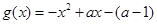 ,根據圖象可得:
,根據圖象可得: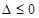 或
或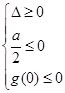 ,解得
,解得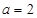 . 11分
. 11分 的取值范圍為
的取值范圍為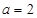 . 12分
. 12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com