
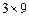 數表
數表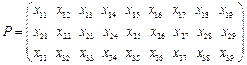
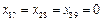 ,
,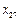 ,
,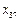 ,
,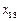 ,
,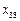 ,
,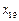 ,
,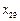 均大于.如果
均大于.如果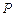 的前三列構成的數表
的前三列構成的數表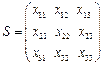
 :對于數表
:對于數表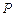 中的任意一列
中的任意一列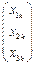 (
(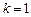 ,2,…,9)均存在某個
,2,…,9)均存在某個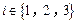
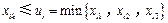 .
.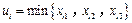 ,
, ,2,3一定自數表
,2,3一定自數表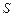 的不同列.
的不同列.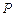 中唯一的一列
中唯一的一列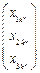 ,
,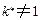 ,2,3使得
,2,3使得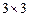 數表
數表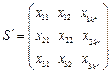
 .
.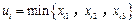 ,
, ,2,3不是取自數表
,2,3不是取自數表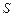 的不同列.則存在一列不含任何
的不同列.則存在一列不含任何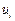 .不妨設
.不妨設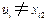 ,
, ,2,3.由于數表
,2,3.由于數表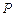 中同一行中的任何兩個元素都不等,于是
中同一行中的任何兩個元素都不等,于是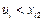 ,
, ,2,3.另一方面,由于數表
,2,3.另一方面,由于數表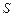 具有性質
具有性質 ,在⑶中取
,在⑶中取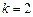 ,則存在某個
,則存在某個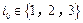 使得
使得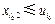 .矛盾.
.矛盾.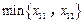 ,
,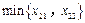 ,
,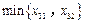
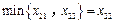 ,
,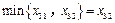 .
.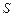 的第一列一定含有某個
的第一列一定含有某個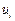 ,所以只能是
,所以只能是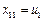 .同樣,第二列中也必含某個
.同樣,第二列中也必含某個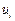 ,
, ,2.不妨設
,2.不妨設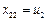 .于是
.于是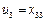 ,即
,即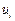 是數表
是數表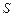 中的對角線上數字.
中的對角線上數字.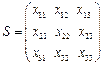
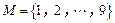 ,令集合
,令集合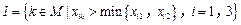 .
.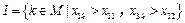 且1,2
且1,2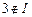 .因為
.因為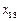 ,
,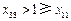 ,
,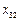 ,所以
,所以 .
.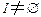 .于是存在
.于是存在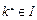 使得
使得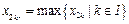 .顯然,
.顯然,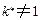 ,2,3.
,2,3.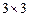 數表
數表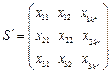
 .
.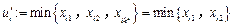 ,
,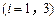 .這說明
.這說明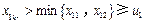 ,
,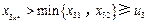 .
.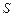 滿足性質
滿足性質 .在⑶中取
.在⑶中取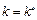 ,推得
,推得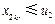 ,于是
,于是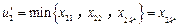 .下證對任意的
.下證對任意的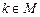 ,存在某個
,存在某個 ,2,3使得
,2,3使得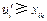 .假若不然,則
.假若不然,則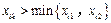 ,
, ,3且
,3且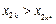 .這與
.這與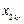 的最大性矛盾.因此,數表
的最大性矛盾.因此,數表 滿足性質
滿足性質 .
.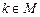 使得數表
使得數表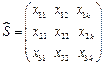
 ,不失一般性,我們假定
,不失一般性,我們假定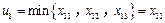
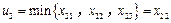
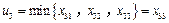
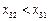 .
.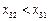 ,
,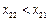 及(ⅰ),有
及(ⅰ),有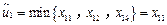 .又由(ⅰ)知:或者
.又由(ⅰ)知:或者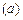
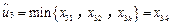 ,或者
,或者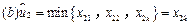 .
.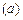 成立,由數表
成立,由數表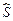 具有性質
具有性質 ,則
,則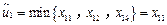 ,
,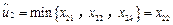 ,
,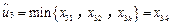 .
.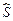 滿足性質
滿足性質 ,則對于
,則對于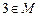 至少存在一個
至少存在一個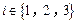 使得
使得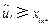 .由
.由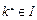 及⑷和⑹式知,
及⑷和⑹式知,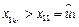 ,
,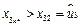 .于是只能有
.于是只能有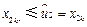 .類似地,由
.類似地,由 滿足性質
滿足性質 及
及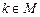 可推得
可推得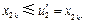 .從而
.從而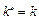 .
.

科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com