(1)設

,求函數(shù)

的最大值;
(2)已知x、y都是正實數(shù),且

,求

的最小值.
(1)

(2)

試題分析:(1)∵

,∴

, ……1分
∴

,當且僅當

即

時,等號成立.
又

……5分
∴函數(shù)

的最大值為

. ……6分
(2)由

得

.
∵x、y都是正實數(shù)
∴

,當且僅當

時,等號成立. ……8分
∴

∴

∴

∴

,當且僅當

時,等號成立. ……10分
聯(lián)立

,解得

……11分
∴當

時,

的最小值是

……12分
點評:應用基本不等式求最值,要注意“一正二定三相等”三個條件缺一不可,另外還要注意一些特殊方法的應用,比如“1”的整體代換等.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
不等式

的解集是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知

,那么下列判斷中正確的是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設

,
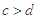
,則下列不等式成立的是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若
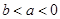
,則下列不等式中正確的是( )
查看答案和解析>>

 ,求函數(shù)
,求函數(shù) 的最大值;
的最大值; ,求
,求 的最小值.
的最小值. 特高級教師點撥系列答案
特高級教師點撥系列答案