
數列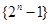 的前
的前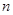 項組成集合
項組成集合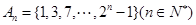 ,從集合
,從集合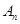 中任取
中任取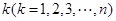 個數,其所有可能的
個數,其所有可能的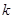 個數的乘積的和為
個數的乘積的和為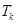 (若只取一個數,規定乘積為此數本身),記
(若只取一個數,規定乘積為此數本身),記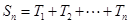 .例如:當
.例如:當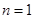 時,
時,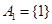 ,
,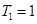 ,
, ;當
;當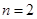 時,
時,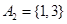 ,
,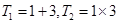 ,
,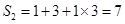 .
.
(Ⅰ)求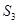 ;
;
(Ⅱ)猜想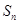 ,并用數學歸納法證明.
,并用數學歸納法證明.
科目:高中數學 來源:2014屆江蘇省高三開學檢測文科數學試卷(解析版) 題型:解答題
數列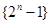 的前
的前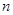 項組成集合
項組成集合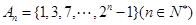 ,從集合
,從集合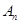 中任取
中任取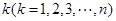 個數,其所有可能的
個數,其所有可能的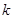 個數的乘積的和為
個數的乘積的和為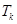 (若只取一個數,規定乘積為此數本身),記
(若只取一個數,規定乘積為此數本身),記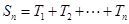 .例如:當
.例如:當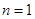 時,
時,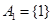 ,
,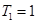 ,
,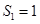 ;當
;當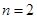 時,
時,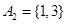 ,
,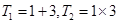 ,
,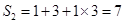 .
.
(Ⅰ)求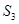 ;
;
(Ⅱ)猜想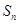 ,并用數學歸納法證明.
,并用數學歸納法證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com