
(本小題滿分12分)已知函數(shù)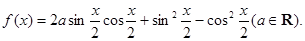
(I)當(dāng)a=1時(shí),求函數(shù)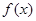 的最小正周期及圖象的對稱軸方程式;
的最小正周期及圖象的對稱軸方程式;
(II)當(dāng)a=2時(shí),在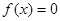 的條件下,求
的條件下,求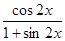 的值.
的值.
(1) 最小正周期為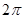 ,
,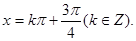 ;(2)
;(2)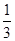 。
。
解析試題分析:(I)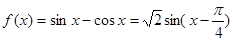
最小正周期為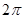 ,
,
由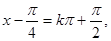
得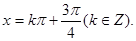 …………6分
…………6分
(II)當(dāng)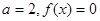 時(shí),解得
時(shí),解得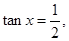
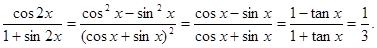 …………12分
…………12分
考點(diǎn):函數(shù)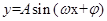 的性質(zhì);二倍角公式。
的性質(zhì);二倍角公式。
點(diǎn)評(píng):三角函數(shù)和其他知識(shí)點(diǎn)相結(jié)合往往是第一道大題,一般較為簡單,應(yīng)該是必得分的題目。而有些同學(xué)在學(xué)習(xí)中認(rèn)為這類題簡單,自己一定會(huì),從而忽略了對它的練習(xí),因此導(dǎo)致考試時(shí)不能得滿分,甚至不能得分。因此我們在平常訓(xùn)練的時(shí)候就要要求自己做到“會(huì)而對,對而全”。


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,摩天輪的半徑為50 m,點(diǎn)O距地面的高度為60 m,摩天輪做勻速轉(zhuǎn)動(dòng),每3 min轉(zhuǎn)一圈,摩天輪上點(diǎn)P的起始位置在最低點(diǎn)處.
(1)試確定在時(shí)刻t(min)時(shí)點(diǎn)P距離地面的高度;
(2)在摩天輪轉(zhuǎn)動(dòng)的一圈內(nèi),有多長時(shí)間點(diǎn)P距離地面超過85 m?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
 為偶函數(shù),其圖象上相鄰兩個(gè)最高點(diǎn)之間的距離為
為偶函數(shù),其圖象上相鄰兩個(gè)最高點(diǎn)之間的距離為 .
.
(1)求函數(shù) 的解析式.
的解析式.
(2)若 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)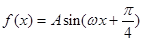 (其中
(其中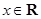 ,
,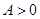 ,
, )的最大值為2,最小正周
)的最大值為2,最小正周
期為 .
.
(1)求函數(shù)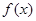 的解析式;
的解析式;
(2)若函數(shù)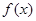 圖象上的兩點(diǎn)
圖象上的兩點(diǎn)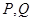 的橫坐標(biāo)依次為
的橫坐標(biāo)依次為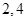 ,
, 為坐標(biāo)原點(diǎn),求△
為坐標(biāo)原點(diǎn),求△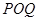 的
的
面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
若向量
 ,其中
,其中 ,記函數(shù)
,記函數(shù) ,若函數(shù)
,若函數(shù) 的圖象與直線
的圖象與直線 為常數(shù))相切,并且切點(diǎn)的橫坐標(biāo)依次成公差為
為常數(shù))相切,并且切點(diǎn)的橫坐標(biāo)依次成公差為 的等差數(shù)列。
的等差數(shù)列。
(1)求 的表達(dá)式及
的表達(dá)式及 的值;
的值;
(2)將函數(shù) 的圖象向左平移
的圖象向左平移 ,得到
,得到 的圖象,當(dāng)
的圖象,當(dāng) 時(shí),
時(shí), 的交點(diǎn)橫坐標(biāo)成等比數(shù)列,求鈍角
的交點(diǎn)橫坐標(biāo)成等比數(shù)列,求鈍角 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知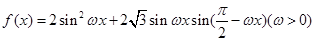 最小正周期為
最小正周期為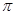
(1).求函數(shù)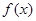 的單調(diào)遞增區(qū)間及對稱中心坐標(biāo)
的單調(diào)遞增區(qū)間及對稱中心坐標(biāo)
(2).求函數(shù)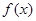 在區(qū)間
在區(qū)間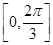 上的取值范圍。
上的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)已知函數(shù)f(x)=cos(- )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的減區(qū)間;
(3)若f(α)= ,α∈(0,
,α∈(0, ),求tan(2α+
),求tan(2α+ )的值.
)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
已知函數(shù)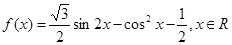
(Ⅰ)求函數(shù)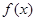 的最小正周期;
的最小正周期;
(Ⅱ)確定函數(shù)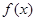 在
在 上的單調(diào)性并求在此區(qū)間上
上的單調(diào)性并求在此區(qū)間上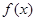 的最小值.
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com