
設(shè)函數(shù)f(x)=ax![]() +bx+1(a,b為實數(shù)),F(x)=
+bx+1(a,b為實數(shù)),F(x)=![]()
(1)若f(-1)=0且對任意實數(shù)x均有f(x)![]() 成立,求F(x)表達(dá)式。
成立,求F(x)表達(dá)式。
(2)在(1)的條件下,當(dāng)x![]() 時,g(x)=f(x)-kx是單調(diào)函數(shù),求實數(shù)k的取值范圍。
時,g(x)=f(x)-kx是單調(diào)函數(shù),求實數(shù)k的取值范圍。
(3)(理)設(shè)m>0,n<0且m+n>0,a>0且f(x)為偶函數(shù),求證:F(m)+F(n)>0。
(1)F(x)=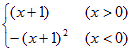 (2)k
(2)k![]() -2或k
-2或k![]() 6(3)見解析
6(3)見解析
(1)![]() f(-1)=0 ∴
f(-1)=0 ∴![]() 由f(x)
由f(x)![]() 0恒成立 知△=b
0恒成立 知△=b![]() -4a=(a+1)
-4a=(a+1)![]() -4a=(a-1)
-4a=(a-1)![]() 0
0
∴a=1從而f(x)=x![]() +2x+1 ∴F(x)=
+2x+1 ∴F(x)=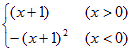 ,
,
(2)由(1)可知f(x)=x![]() +2x+1 ∴g(x)=f(x)-kx=x
+2x+1 ∴g(x)=f(x)-kx=x![]() +(2-k)x+1,由于g(x)在
+(2-k)x+1,由于g(x)在![]() 上是單調(diào)函數(shù),知-
上是單調(diào)函數(shù),知-![]() 或-
或-![]() ,得k
,得k![]() -2或k
-2或k![]() 6 ,
6 ,
(3)![]() f(x)是偶函數(shù),∴f(x)=f(x),而a>0∴
f(x)是偶函數(shù),∴f(x)=f(x),而a>0∴![]() 在
在![]() 上為增函數(shù)
上為增函數(shù)
對于F(x),當(dāng)x>0時-x<0,F(xiàn)(-x)=-f(-x)=-f(x)=-F(x),當(dāng)x<0時-x>0,F(xiàn)(-x)=f(-x)=f(x)=-F(x),
∴F(x)是奇函數(shù)且F(x)在![]() 上為增函數(shù),
上為增函數(shù),
![]() m>0,n<0,由m>-n>0知F(m)>F(-n)∴F(m)>-F(n)
m>0,n<0,由m>-n>0知F(m)>F(-n)∴F(m)>-F(n)
∴F(m)+F(n)>0 。


科目:高中數(shù)學(xué) 來源: 題型:
| a+1 |
| x |
| m |
| x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| b | x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| ax-1 | x+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| b | x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| b | x |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com