
已知A、B、C是橢圓 上的三點,其中點A的坐標為
上的三點,其中點A的坐標為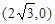 ,BC過橢圓m的中心,且
,BC過橢圓m的中心,且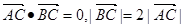
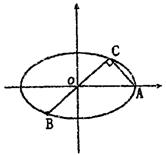
(1)求橢圓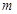 的方程;
的方程;
(2)過點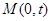 的直線l(斜率存在時)與橢圓m交于兩點P,Q,
的直線l(斜率存在時)與橢圓m交于兩點P,Q,
設D為橢圓m與y軸負半軸的交點,且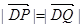 ,求實數t的取值范圍.
,求實數t的取值范圍.
(1)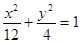 (2)t∈(-2,4)
(2)t∈(-2,4)
【解析】本題考查橢圓的標準方程,考查直線與橢圓的位置關系,解題的關鍵是將 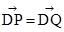 轉化為kDN•k=-1進行求解.
轉化為kDN•k=-1進行求解.
(1)根據橢圓的性質和向量的數量積為零得到a,b的值,得到橢圓的方程。
(2)設出直線與橢圓聯立方程組,然后結合根與系數的關系,和向量的等式得到參數的關系式,進而利用判別式得到范圍。
解(1)∵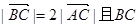 過(0,0)
過(0,0)
則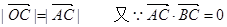
∴∠OCA=90°, 即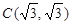 又∵
又∵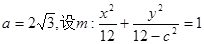
將C點坐標代入得 
解得 c2=8,b2=4
∴橢圓m: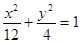
(2)由條件D(0,-2) ∵M(0,t)
1°當k=0時,顯然-2<t<2
2°當k≠0時,設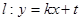
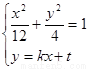 消y得
消y得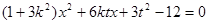
由△>0 可得 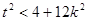 ①
①
設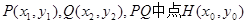
則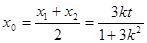
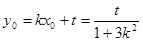
∴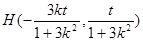
由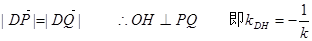
∴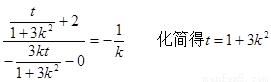 ②
②
∴t>1 將①代入②得 1<t<4
∴t的范圍是(1,4)
綜上t∈(-2,4)


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| AC |
| BC |
| BC |
| AC |
| DP |
| DQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
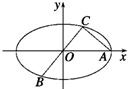 如圖所示,已知A,B,C是橢圓E:
如圖所示,已知A,B,C是橢圓E:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| PQ |
| AB |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| AC |
| BC |
| BC |
| AC |
| DP |
| DQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
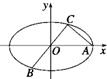 如圖所示,已知A、B、C是橢圓E:
如圖所示,已知A、B、C是橢圓E:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com