
(本小題共12分)
如圖,已知直線l與拋物線 相切于點P(2,1),且與x軸交于點A,O為坐標原點,
相切于點P(2,1),且與x軸交于點A,O為坐標原點,
定點B的坐標為(2,0).

(1)若動點M滿足 ,求點M的軌跡C;
,求點M的軌跡C;
(2)若過點B的直線l′(斜率不等于零)與(I)中的軌跡C交于不同的兩點E、F(E在B、F之間),試求△OBE與△OBF面積之比的取值范圍.
(I)動點M的軌跡C為以原點為中心,焦點在x軸上,長軸長為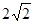 ,短軸長為2的橢圓
(II)(3-2
,短軸長為2的橢圓
(II)(3-2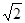 ,1).
,1).
【解析】
試題分析:(I)由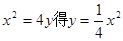 ,
, 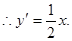 ∴直線l的斜率為
∴直線l的斜率為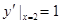
故l的方程為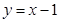 ,∴點A坐標為(1,0)
,∴點A坐標為(1,0)
設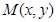 則
則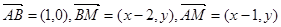 ,
,
由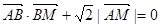 得
得 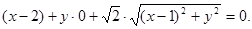
整理,得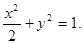
∴動點M的軌跡C為以原點為中心,焦點在x軸上,長軸長為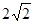 ,短軸長為2的橢圓
,短軸長為2的橢圓
(II)由題意知直線l的斜率存在且不為零,設l方程為y=k(x-2)(k≠0)①
將①代入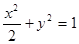 ,整理,得
,整理,得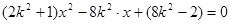 ,
,
由△>0得0<k2<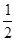 . 設E(x1,y1),F(x2,y2)
. 設E(x1,y1),F(x2,y2)
則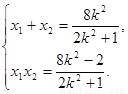 ②
②
令 ,由此可得
,由此可得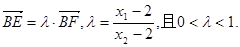
由②知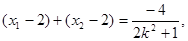
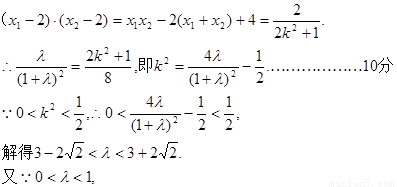
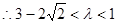 .
.
∴△OBE與△OBF面積之比的取值范圍是(3-2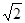 ,1).
,1).
考點:本題考查了直線與拋物線的位置關系
點評:對于直線與圓錐曲線的綜合問題,往往要聯立方程,同時結合一元二次方程根與系數的關系進行求解;而對于最值問題,則可將該表達式用直線斜率k表示,然后根據題意將其進行化簡結合表達式的形式選取最值的計算方式.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
. (本小題共12分)已知橢圓E:![]() 的焦點坐
的焦點坐![]() 標為
標為![]() (
(![]() ),點M(
),點M(![]() ,
,![]() )在橢圓E上
)在橢圓E上![]() (1)求橢圓E的方程;(2)O為坐標原點,⊙
(1)求橢圓E的方程;(2)O為坐標原點,⊙![]() 的任意一條切線與橢圓E有兩個交點
的任意一條切線與橢圓E有兩個交點![]() ,
,![]() 且
且![]() ,求⊙
,求⊙![]() 的半徑。
的半徑。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古呼倫貝爾市高三第三次模擬考試文科數學試卷 題型:解答題
(本小題共12分)如圖,已知 ⊥平面
⊥平面 ,
, ∥
∥ ,
, 是正三角形,
是正三角形, ,且
,且 是
是 的中點
的中點

(1)求證: ∥平面
∥平面 ;
;
(2)求證:平面BCE⊥平面 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古呼倫貝爾市高三第三次模擬考試文科數學試卷 題型:解答題
(本小題共12分)某中學的高二(1)班男同學有 名,女同學有
名,女同學有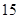 名,老師按照分層抽樣的方法組建了一個
名,老師按照分層抽樣的方法組建了一個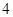 人的課外興趣小組.
人的課外興趣小組.
(Ⅰ)求某同學被抽到的概率及課外興趣小組中男、女同學的人數;
(Ⅱ)經過一個月的學習、討論,這個興趣小組決定選出兩名同學做某項實驗,方法是先從小組里選出 名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
查看答案和解析>>
科目:高中數學 來源:2010-2011學年甘肅省天水市高三上學期第一階段性考試理科數學卷 題型:解答題
(本小題共12分)
如圖,在正三棱柱ABC—A1B1C1中,點D是棱AB的中點,BC=1,AA1=
(1)求證:BC1//平面A1DC;
(2)求二面角D—A1C—A的大小

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com