本試題主要是考查了等差數列在實際生活中的運用。等差數列的通項公式和前n項和,以及等比數列的通項公式的運用。
(1)分析出中低價房面積形成數列{a
n},由題意可知{a
n}是等差數列,其中a
1=250,d=50,可知前n項和。結合不等式得到結論。
(2)根據題意可知新建住房面積形成數列{b
n},由題意可知 {b
n}是等比數列,其中b
1=400,q=1.08,,然后借助于等比數列的知識解決。
(1)設中低價房面積形成數列{a
n},由題意可知{a
n}是等差數列,其中a
1=250,d=50,則S
n= 250n+
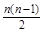
×50=25n
2+225n, 令25n
2+225n≥4750,即n
2+9n-190≥0,而n是正整數,∴n≥10.到 2020年底,該市歷年所建中低價房的累計面積將首次不少于4750萬平方米.
(2)設新建住房面積形成數列{b
n},由題意可知 {b
n}是等比數列,其中b
1=400,q=1.08,則b
n=400·(1.08)
n-1·0.85.由題意可知a
n>0.85b
n,有
250+ (n-1)·50>400·(1.08)
n-1·0.85,即20+ 5n>34(1.08)
n-1 ,即4+ n>6.8(1.08)
n-1經檢驗,滿足上述不等式的最小正整數n=6.到2016年底,當年建造的中低價房的面積占該年建造住房面積的比例首次大于85%.

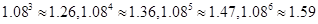 )
)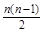 ×50=25n2+225n, 令25n2+225n≥4750,即n2+9n-190≥0,而n是正整數,∴n≥10.到 2020年底,該市歷年所建中低價房的累計面積將首次不少于4750萬平方米.
×50=25n2+225n, 令25n2+225n≥4750,即n2+9n-190≥0,而n是正整數,∴n≥10.到 2020年底,該市歷年所建中低價房的累計面積將首次不少于4750萬平方米. 

 閱讀快車系列答案
閱讀快車系列答案