
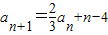 ,bn=(-1)n(an-3n+21),其中λ為實數,n為正整數.
,bn=(-1)n(an-3n+21),其中λ為實數,n為正整數.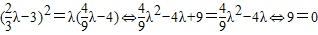 ,矛盾.
,矛盾. an-2n+14)=-
an-2n+14)=- (-1)n•(an-3n+21)=-
(-1)n•(an-3n+21)=- bn
bn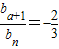 (n∈N+).
(n∈N+). 為公比的等比數列.bn=-(λ+18)•(-
為公比的等比數列.bn=-(λ+18)•(- )n-1.
)n-1. )n-1,
)n-1,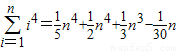 ,
, (λ+18)•[1-(-
(λ+18)•[1-(- )n]<a+1(n∈N+)得
)n]<a+1(n∈N+)得 ①
① ,則
,則 ,
, ,f(n)的最小值為f(2)=
,f(n)的最小值為f(2)= ,
, a<-
a<- (λ+18)
(λ+18) ,即得-(a+1)-18<λ<-3a-18.
,即得-(a+1)-18<λ<-3a-18. .
.

 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省鹽城市東臺中學高三(上)期中數學試卷(解析版) 題型:填空題
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省黃岡市黃州一中高三(上)10月月考數學試卷(理科)(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com