
��D���^(gu��)�c(di��n)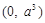 �ă�ֱ���c���タ
�ă�ֱ���c���タ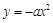 ������A��B���c(di��n)�� AD��BC��ֱ��ֱ��
������A��B���c(di��n)�� AD��BC��ֱ��ֱ��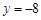 ������քe��D��C��
������քe��D��C��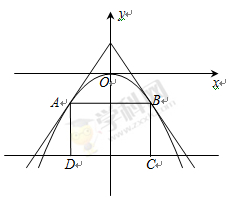
��1����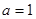 �������ABCD��e��
�������ABCD��e��
��2����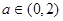 �������ABCD��e�����ֵ��
�������ABCD��e�����ֵ��
��1��14 ��2��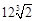
����ԇ�}��������1����(d��ng)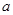 =1�r(sh��)�����O(sh��)�о���y=kx+1,(li��n)��
=1�r(sh��)�����O(sh��)�о���y=kx+1,(li��n)��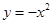 .���Єeʽ��������k�����c(di��n)����(bi��o).���������e.��2�����O(sh��)���c(di��n)����(du��)���タ��(d��o)���б�ʌ����о����̣����붨�c(di��n)(0,
.���Єeʽ��������k�����c(di��n)����(bi��o).���������e.��2�����O(sh��)���c(di��n)����(du��)���タ��(d��o)���б�ʌ����о����̣����붨�c(di��n)(0, 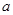 )������c(di��n)����(bi��o)����
)������c(di��n)����(bi��o)����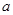 ��.������e�ı��_(d��)ʽ.����(j��)
��.������e�ı��_(d��)ʽ.����(j��)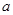 �ķ������S�����ֵ.���}�dz�Ҋ��ֱ���c���タ���P(gu��n)ϵ���}��.�O(sh��)���c(di��n)��(li��n)�������ҳ��P(gu��n)�����c(di��n)�ĵ�ʽ.ͨ�^(gu��)��(du��)����(sh��)
�ķ������S�����ֵ.���}�dz�Ҋ��ֱ���c���タ���P(gu��n)ϵ���}��.�O(sh��)���c(di��n)��(li��n)�������ҳ��P(gu��n)�����c(di��n)�ĵ�ʽ.ͨ�^(gu��)��(du��)����(sh��)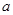 �ķ���������(y��ng)�����ֵ.
�ķ���������(y��ng)�����ֵ.
ԇ�}��������1��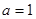 �r(sh��)��
�r(sh��)��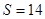 ��Ԕ��(x��)�^(gu��)��Ҋ�ڣ�2����(w��n)�� 6��
��Ԕ��(x��)�^(gu��)��Ҋ�ڣ�2����(w��n)�� 6��
��2���O(sh��)���c(di��n)��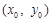 ���t
���t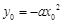 ,
,
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/ae/7/rjb5h1.png" style="vertical-align:middle;" />�������о����̞�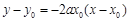 , ��
, ��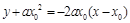 ��
��
��?y��n)���^(gu��)�c(di��n)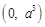 ������
������ ����
����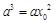 ������
������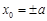 ��
��
��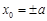 ����
����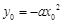 ��
��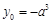 ��
��
(���O(sh��)�о����̞�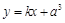 �����뒁�タ���̺���
�����뒁�タ���̺���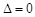 �õ����c(di��n)����(bi��o)�������J(r��n)�ɣ�)
�õ����c(di��n)����(bi��o)�������J(r��n)�ɣ�)
����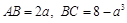 �� ���Ծ�����e��
�� ���Ծ�����e��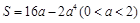 ��
��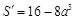 ��
��
���Ԯ�(d��ng)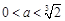 �r(sh��)��
�r(sh��)��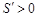 ����(d��ng)
����(d��ng)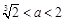 �r(sh��)��
�r(sh��)��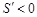 ��
��
�ʮ�(d��ng)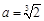 �r(sh��)��S�����ֵ��
�r(sh��)��S�����ֵ��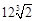 �� 15��
�� 15��
���c(di��n)��1.ֱ���c���タ���P(gu��n)ϵ.2.���һ���˼�S��ʽ.3.��(d��o)��(sh��)����ֵ.


 �п����x���c(di��n)����ϵ�д�
�п����x���c(di��n)����ϵ�д� ������ĩ��(f��)��(x��)��Ӗ(x��n)��ϵ�д�
������ĩ��(f��)��(x��)��Ӗ(x��n)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A ��������ԭ�c(di��n)�����c(di��n)��
��������ԭ�c(di��n)�����c(di��n)�� �S�ϣ��ԃɂ�(g��)���c(di��n)�Ͷ��S�ăɂ�(g��)���c(di��n)����c(di��n)����߅����һ��(g��)��e��
�S�ϣ��ԃɂ�(g��)���c(di��n)�Ͷ��S�ăɂ�(g��)���c(di��n)����c(di��n)����߅����һ��(g��)��e��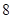 �������Σ�ӛ��
�������Σ�ӛ��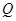 ��
��
������E�A �ķ���
�ķ���
�����O(sh��)�c(di��n) ��ֱ��
��ֱ��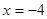 �c
�c �S�Ľ��c(di��n)���^(gu��)�c(di��n)
�S�Ľ��c(di��n)���^(gu��)�c(di��n) ��ֱ��
��ֱ�� �c�E�A
�c�E�A �ཻ��
�ཻ��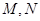 ���c(di��n)����(d��ng)����
���c(di��n)����(d��ng)����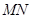 �����c(di��n)����������
�����c(di��n)����������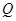 ��(n��i)������߅�磩�r(sh��)����ֱ��
��(n��i)������߅�磩�r(sh��)����ֱ�� б�ʵ�ȡֵ����
б�ʵ�ȡֵ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�A�F����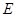 �ăɂ�(g��)���c(di��n)����(bi��o)��
�ăɂ�(g��)���c(di��n)����(bi��o)��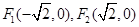 �����x���ʞ�
�����x���ʞ�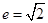 ��
��
����������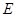 �ķ��̣�
�ķ��̣�
�����O(sh��)����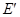 ��ʾ����
��ʾ����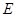 ��
��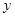 �S��߅���֣���ֱ��
�S��߅���֣���ֱ��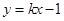 �c����
�c����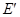 �ཻ��
�ཻ��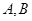 ���c(di��n)����
���c(di��n)����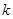 ��ȡֵ������
��ȡֵ������
�����ڗl�������£����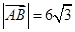 ��������
��������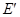 �ϴ����c(di��n)
�ϴ����c(di��n)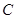 ��ʹ
��ʹ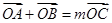 ����
����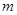 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A ���x���ʞ�
���x���ʞ� �������c(di��n)
�������c(di��n) ���c(di��n)
���c(di��n) �ľ��x��
�ľ��x�� .
.
��1����E�A�ķ��̣�
��2���^(gu��)�ҽ��c(di��n)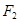 ��ֱ���c�E�A���ڲ�ͬ�ă��c(di��n)
��ֱ���c�E�A���ڲ�ͬ�ă��c(di��n) ��
��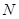 ���t
���t ��(n��i)�ЈA�ĈA��e�Ƿ�������ֵ�������ڣ�����@��(g��)���ֵ���˕r(sh��)��ֱ�����̣��������ڣ�Ո(q��ng)�f(shu��)������.
��(n��i)�ЈA�ĈA��e�Ƿ�������ֵ�������ڣ�����@��(g��)���ֵ���˕r(sh��)��ֱ�����̣��������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A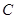 ��������ԭ�c(di��n)
��������ԭ�c(di��n)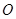 ,�x����
,�x����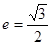 ,�ҽ��c(di��n)��
,�ҽ��c(di��n)��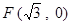 .
.
(��)��E�A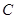 �ķ���;
�ķ���;
(��)�O(sh��)�E�A������c(di��n)��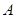 ,�ڙE�A
,�ڙE�A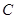 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)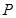 ,ʹ������
,ʹ������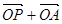 �c
�c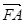 ����?������,��ֱ��
����?������,��ֱ��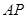 �ķ���;��������,��(ji��n)Ҫ�f(shu��)������.
�ķ���;��������,��(ji��n)Ҫ�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�c(di��n) ��
��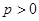 ��
��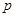 �dz���(sh��)�����҄�(d��ng)�c(di��n)
�dz���(sh��)�����҄�(d��ng)�c(di��n)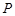 ��
��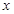 �S�ľ��x�ȵ��c(di��n)
�S�ľ��x�ȵ��c(di��n)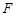 �ľ��xС
�ľ��xС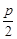 .
.
��1�����(d��ng)�c(di��n)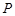 ��܉�E
��܉�E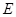 �ķ��̣�
�ķ��̣�
��2����i����֪�c(di��n) ��������
�������� �ϴ��ڲ�ͬ���c(di��n)
�ϴ��ڲ�ͬ���c(di��n) ��
�� �M��
�M��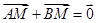 ����(sh��)��(sh��)
����(sh��)��(sh��)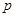 ��ȡֵ������
��ȡֵ������
��ii����(d��ng) �r(sh��)�����タ
�r(sh��)�����タ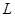 ���Ƿ���ڮ���
���Ƿ���ڮ��� ��
�� ���c(di��n)
���c(di��n) ��ʹ�ý�(j��ng)�^(gu��)
��ʹ�ý�(j��ng)�^(gu��) ��
�� ��
�� ���c(di��n)�ĈA�͒��タ
���c(di��n)�ĈA�͒��タ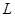 ���c(di��n)
���c(di��n) ̎����ͬ���о��������ڣ�����c(di��n)
̎����ͬ���о��������ڣ�����c(di��n) ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A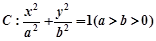 �Ľ��c(di��n)��
�Ľ��c(di��n)��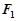
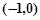 ��
��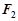
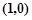 ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n)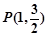 .
.
������E�A �ķ��̣�
�ķ��̣�
�����O(sh��)�^(gu��)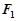 ��ֱ��
��ֱ�� �c�E�A
�c�E�A ����
����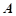 ��
�� ���c(di��n)����(w��n)�ڙE�A
���c(di��n)����(w��n)�ڙE�A ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n) ��ʹ��߅��
��ʹ��߅��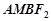 ��ƽ����߅�Σ������ڣ����ֱ��
��ƽ����߅�Σ������ڣ����ֱ�� �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ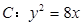 ��
��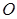 ������(bi��o)ԭ�c(di��n)����(d��ng)ֱ��
������(bi��o)ԭ�c(di��n)����(d��ng)ֱ��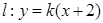 �c
�c
���タ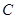 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)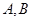
��1�����C: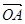 ��
��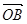 �鳣��(sh��)��
�鳣��(sh��)��
��2����M��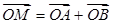 ���c(di��n)
���c(di��n)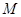 ��܉�E���̡�
��܉�E���̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���c(di��n)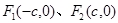 �քe�ǙE�AC:
�քe�ǙE�AC: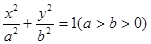 �����ҽ��c(di��n)���^(gu��)�c(di��n)
�����ҽ��c(di��n)���^(gu��)�c(di��n)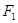 ��
��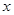 �S�Ĵ��������E�A
�S�Ĵ��������E�A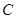 ���ϰ벿�����c(di��n)
���ϰ벿�����c(di��n)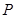 ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)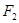 ��
��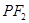 �Ĵ�����ֱ��
�Ĵ�����ֱ�� ���c(di��n)
���c(di��n) .
.
��1������c(di��n) ������(bi��o)�飨4,4������E�A
������(bi��o)�飨4,4������E�A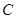 �ķ��̣�
�ķ��̣�
��2��ԇ�Д�ֱ��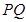 �c�E�A
�c�E�A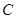 �Ĺ����c(di��n)��(g��)��(sh��)�����C����ĽY(ji��)Փ.
�Ĺ����c(di��n)��(g��)��(sh��)�����C����ĽY(ji��)Փ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com