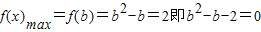已知函數f(x)=-x2+2bx-b
(1)當b=2時,求函數y=f(x) 在[1,4]上的最值;
(2)若函數y=f(x) 在[1,4]上僅有一個零點,求b的取值范圍;
(3)是否存在實數b,使得函數y=f(x) 在[1,+∞)上的最大值是2,若存在,求出b的值;若不存在,請說明理由.
【答案】
分析:(1)當b=2時,函數y=f(x)的圖象為開口向下,對稱軸為x=2的拋物線,故函數y=f(x) 在[1,2]上為增函數,在[2,4]上為減函數,由此判斷出最值,求出即可;
(2)若函數y=f(x) 在[1,4]上僅有一個零點,則f(1)•f(4)≤0,由此構造關于b的不等式,解不等式可得b的取值范圍;
(3)分b<1時,和b≥1時,結合 二次函數的圖象和性質分析出函數的最大值為2時,對應的b值,最后綜合討論結果,可得答案.
解答:解:f(x)=-x
2+2bx-b=-(x-b)
2-b+b
2,的圖象開口向下,對稱軸為x=b的拋物線…(1分)
(1)當b=2時,f(x)=-x
2+4x-2=-(x-2)
2+2的圖象開口向下,對稱軸為x=2…(2分)
∴f(x)
max=f(2)=2,
f(x)
min=f(4)=-2…(4分)
(2)∵函數y=f(x) 在[1,4]上僅有一個零點
∴f(1)•f(4)≤0…(6分)(須驗證端點是否成立與△=0的情況)
即(-1+b)(-16+7b)≤0
∴
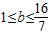
∴b的取值范圍是
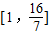
…(7分)
(3)當b<1時,y=f(x) 在[1,+∞)上是減函數,
f(x)
max=f(1)=b-1=2
解得b=3,不合要求…(9分)
當b≥1時,
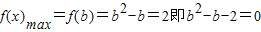
解得b=2或b=-1(不合,舍去),
∴b=2…(11分)
綜上所述,當b=2時,使得函數y=f(x) 在[1,+∞)上的最大值是2.…(12分)
點評:本題考查的知識點是二次函數在閉區間上的最值,函數的值域,函數的零點,熟練掌握二次函數的圖象和性質是解答的關鍵.

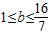
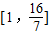 …(7分)
…(7分)