若實數a,b滿足a2+b2=1且c<a+b,恒成立,則c的取值范圍是 .
【答案】
分析:c<a+b恒成立,只須c小于a+b的最小值即可.可利用基本不等式a
2+b
2≥2ab得到:2(a
2+b
2)≥2ab+a
2+b
2=(a+b)
2,從而可求得a+b的取值范圍.
解答:解:∵a
2+b
2=1,
∴由基本不等式a
2+b
2≥2ab得:2(a
2+b
2)≥2ab+a
2+b
2=(a+b)
2,
即(a+b)
2≤2(a
2+b
2)=2,
∴-
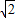
≤a+b≤

,
若c<a+b恒成立,則c<(a+b)的最小值-
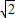
.即c
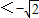
.
故答案為:c

.
點評:本題考查基本不等式,難點在于尋找已知條件a
2+b
2=1與所求a+b(的取值范圍)之間的聯系,即(a+b)
2≤2(a
2+b
2),當然也可以利用圓的參數方程,借助三角函數的輔助角公式來解決,屬于中檔題.

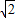 ≤a+b≤
≤a+b≤ ,
,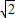 .即c
.即c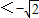 .
. .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案