
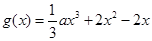 ,函數
,函數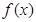 是函數
是函數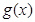 的導函數.
的導函數.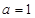 ,求
,求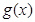 的單調減區間;
的單調減區間;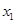 ,
,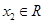 且
且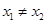 ,都有
,都有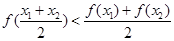 ,求實數
,求實數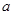 的取值范圍;
的取值范圍;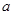 的范圍內,若存在一個與
的范圍內,若存在一個與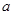 有關的負數
有關的負數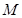 ,使得對任意
,使得對任意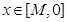 時
時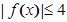 恒成立,求
恒成立,求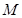 的最小值及相應的
的最小值及相應的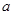 值.
值.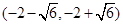 (2)
(2)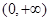 (3)當
(3)當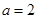 時,
時,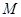 的最小值為
的最小值為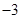
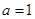 時,
時, ,
,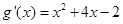 ……………1分
……………1分 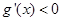 解得
解得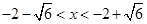 ………………2分
………………2分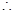 當
當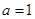 時函數
時函數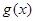 的單調減區間為
的單調減區間為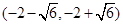 ;…………3分
;…………3分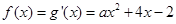
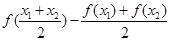
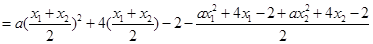
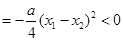 ……………………………………………………5分
……………………………………………………5分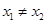 ,所以
,所以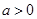 ,即實數
,即實數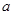 的取值范圍是
的取值范圍是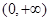 ;…………6分
;…………6分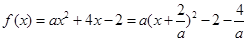 ,
,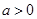 .
.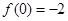 ,由(2)知拋物線的對稱軸
,由(2)知拋物線的對稱軸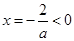 …………7分
…………7分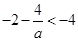 即
即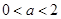 時,
時,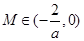 且
且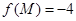
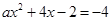 解得
解得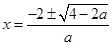 ………………8分
………………8分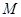 取較大的根,即
取較大的根,即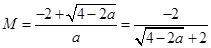 ……………9分
……………9分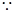
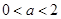 ,
, 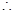
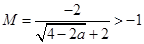 …………………10分
…………………10分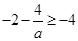 即
即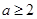 時,
時,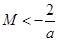 且
且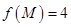
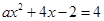 解得
解得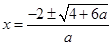 ………………11分
………………11分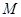 取較小的根,即
取較小的根,即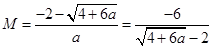 …………12分
…………12分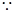
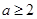 ,
, 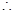
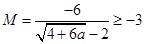 當且僅當
當且僅當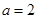 時取等號……13分
時取等號……13分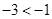 ,所以當
,所以當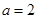 時,
時,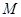 取得最小值
取得最小值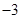 ………………14分
………………14分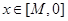 時,“
時,“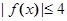 恒成立”等價于“
恒成立”等價于“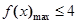 且
且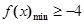 ”
”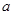 的取值范圍是
的取值范圍是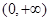
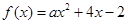 的圖象是開口向上,對稱軸
的圖象是開口向上,對稱軸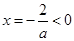 的拋物線…7分
的拋物線…7分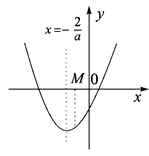
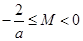 時,
時,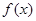 在區間
在區間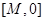 上單調遞增,
上單調遞增,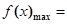
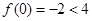 ,
,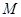 最小,只需要
最小,只需要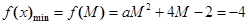 ………8分
………8分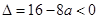 即
即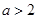 時,無解
時,無解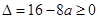 即
即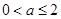 時,………………9分
時,………………9分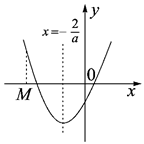
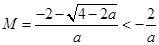 (舍去) 或
(舍去) 或
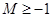 (當且僅當
(當且僅當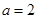 時取等號)…………10分
時取等號)…………10分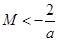 時,
時,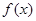 在區間
在區間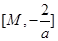 上單調遞減,在
上單調遞減,在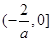 遞增,
遞增,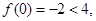
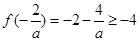 則
則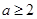 ,…………………11分
,…………………11分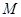 最小,則
最小,則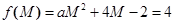 即
即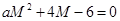 ………………………………………………………12分
………………………………………………………12分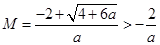 (舍去)
(舍去)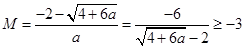 (當且僅當
(當且僅當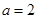 時取等號)…13分
時取等號)…13分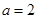 時,
時,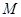 的最小值為
的最小值為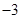 .………………………………14分
.………………………………14分

科目:高中數學 來源:不詳 題型:解答題
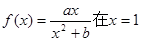 處取得極值2
處取得極值2 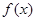 的表達式;
的表達式;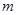 滿足什么條件時,函數
滿足什么條件時,函數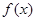 在區間
在區間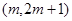 上單調遞增?
上單調遞增?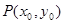 為
為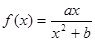 圖象上任意一點,直線與
圖象上任意一點,直線與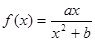 的圖象相切于點P,求直線的斜率
的圖象相切于點P,求直線的斜率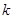 的取值范圍
的取值范圍 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
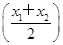 >0.
>0.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
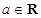 ,函數
,函數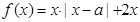 .
.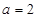 ,求函數
,求函數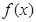 在區間
在區間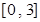 上的最大值;
上的最大值;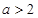 ,寫出函數
,寫出函數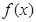 的單調區間(不必證明);
的單調區間(不必證明);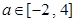 ,使得關于
,使得關于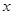 的方程
的方程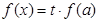 有三個不相等的實數解,求實數
有三個不相等的實數解,求實數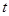 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.(0,+∞) | B.(-1,0)∪(2,+∞) |
| C.(2,+∞) | D.(-1,0) |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com