
已知關于x的函數f(x)=![]() +bx2+cx+bc,其導函數為f+(x).令g(x)=∣f (x) ∣,記函數g(x)在區間[-1、1]上的最大值為M.
+bx2+cx+bc,其導函數為f+(x).令g(x)=∣f (x) ∣,記函數g(x)在區間[-1、1]上的最大值為M.
(Ⅰ)如果函數f(x)在x=1處有極值-![]() ,試確定b、c的值:
,試確定b、c的值:
(Ⅱ)若∣b∣>1,證明對任意的c,都有M>2: w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅲ)若M≧K對任意的b、c恒成立,試求k的最大值。
(Ⅰ) ![]() (Ⅱ)略(Ⅲ)
(Ⅱ)略(Ⅲ)![]()
本小題主要考察函數、函數的導數和不等式等基礎知識,考察綜合運用數學知識進行推理論證的能力和份額類討論的思想(滿分14分)
(I)解:![]() ,由
,由![]() 在
在![]() 處有極值
處有極值![]()
可得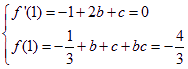
解得![]() 或
或![]()
若![]() ,則
,則![]() ,此時
,此時![]() 沒有極值;
沒有極值;
若![]() ,則
,則![]()
當![]() 變化時,
變化時,![]() ,
,![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
| 1 |
|
|
|
| 0 | + | 0 |
|
|
|
| 極小值 |
| 極大值 |
|
![]() 當
當![]() 時,
時,![]() 有極大值
有極大值![]() ,故
,故![]() ,
,![]() 即為所求。
即為所求。
(Ⅱ)證法1:![]()
當![]() 時,函數
時,函數![]() 的對稱軸
的對稱軸![]() 位于區間
位于區間![]() 之外。
之外。
![]() 在
在![]() 上的最值在兩端點處取得
上的最值在兩端點處取得
故![]() 應是
應是![]() 和
和![]() 中較大的一個
中較大的一個
![]() 即
即![]()
證法2(反證法):因為![]() ,所以函數
,所以函數![]() 的對稱軸
的對稱軸![]() 位于區間
位于區間![]() 之外,
之外,
![]() 在
在![]() 上的最值在兩端點處取得。
上的最值在兩端點處取得。
故![]() 應是
應是![]() 和
和![]() 中較大的一個
中較大的一個
假設![]() ,則
,則
![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
將上述兩式相加得:
![]() ,導致矛盾,
,導致矛盾,![]()
(Ⅲ)解法1:![]()
(1)當![]() 時,由(Ⅱ)可知
時,由(Ⅱ)可知![]() ;
;
(2)當![]() 時,函數
時,函數![]() )的對稱軸
)的對稱軸![]() 位于區間
位于區間![]() 內,w.w.w.k.s.5.u.c.o.m
內,w.w.w.k.s.5.u.c.o.m ![]()
![]()
此時![]()
由![]() 有
有![]()
①若![]() 則
則![]() ,
,
于是![]()
②若![]() ,則
,則![]()
![]()
于是![]()
綜上,對任意的![]() 、
、![]() 都有
都有![]()
而當![]() 時,
時,![]() 在區間
在區間![]() 上的最大值
上的最大值![]()
故![]() 對任意的
對任意的![]() 、
、![]() 恒成立的
恒成立的![]() 的最大值為
的最大值為![]() 。
。
解法2:![]()
(1)當![]() 時,由(Ⅱ)可知
時,由(Ⅱ)可知![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)當![]() 時,函數
時,函數![]() 的對稱軸
的對稱軸![]() 位于區間
位于區間![]() 內,
內,
此時![]()
![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ,即
,即![]()
下同解法1


 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| b |
| a |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com