
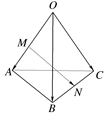
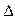 ABC的邊長為1,AE
ABC的邊長為1,AE 平面ABC,CD∥AE,且CD=
平面ABC,CD∥AE,且CD=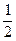 AE.
AE.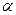 ,AE=
,AE=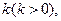 若
若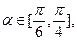 求
求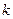 的取值范圍;
的取值范圍;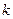 取得最大值時,求平面BDE與平面ABC所成角的大小.
取得最大值時,求平面BDE與平面ABC所成角的大小.

 方法一:
方法一: 中點
中點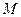 ,連結(jié)
,連結(jié)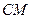 、
、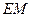 ,由
,由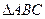 為正三角形,得
為正三角形,得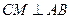 ,又
,又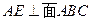 ,則
,則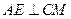 ,可知
,可知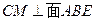 ,所以
,所以 為
為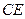 與平面
與平面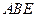 所成角.……………2分
所成角.……………2分 ,……………4分
,……………4分 ,得
,得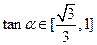 ,得
,得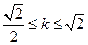 .……………6分
.……………6分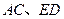 交于點S,連
交于點S,連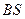 ,
,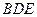
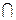 平面
平面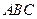 =
=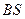 .………………………7分
.………………………7分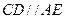 ,且
,且 ,又因為
,又因為 =1,從而
=1,從而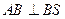 ,…………………8分
,…………………8分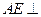 面
面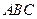 ,由三垂線定理可知
,由三垂線定理可知 ,即
,即 為平面
為平面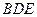 與平面
與平面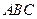 所成的角;……………………10分
所成的角;……………………10分 ,
,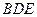 與面
與面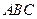 所成的角的大小為
所成的角的大小為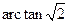 .………………12分
.………………12分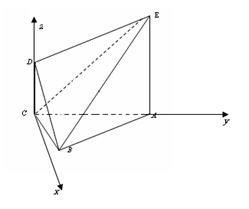 解:
解: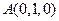 ,
,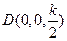 ,
,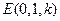 ,
,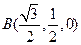 .……………2分
.……………2分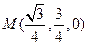 ,
,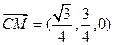 ,
,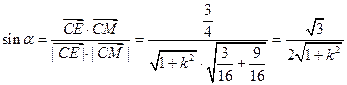 .………………4分
.………………4分 ,則
,則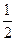
 ,
, 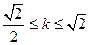 .…………………6分
.…………………6分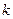 最大值為
最大值為 ,則當(dāng)
,則當(dāng)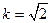 時,設(shè)平面BDE法向量為
時,設(shè)平面BDE法向量為 ,則
,則
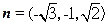 ,………………8分
,………………8分 ,……………………10分
,……………………10分 =
=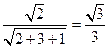 ,
,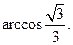 ……………………12分
……………………12分

 科學(xué)實驗活動冊系列答案
科學(xué)實驗活動冊系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
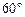 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中點,F(xiàn)是AB的中點.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中點,F(xiàn)是AB的中點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
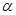 ,
,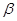 ,
,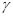 兩兩互相垂直,點
兩兩互相垂直,點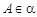 ,點
,點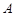 到
到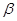 ,
,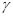 的距離都是
的距離都是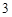 ,點
,點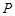 是
是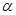 上的動點,滿足
上的動點,滿足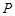 到
到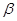 的距離是到
的距離是到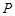 到點
到點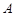 距離的
距離的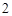 倍,則點
倍,則點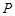 的軌跡上的點到
的軌跡上的點到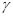 的距離的最小值為
的距離的最小值為A.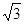 | B.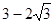 |
C.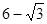 | D.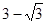 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.-a+ b+c b+c | B.a(chǎn)-b+c | C.a(chǎn)+b-c | D.a(chǎn)+b-c |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
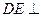 平面ABCD,
平面ABCD,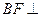 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
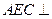 平面AFC。
平面AFC。查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com