
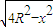 .利用公式表示成圓柱體的體積,利用導數求最值即可.
.利用公式表示成圓柱體的體積,利用導數求最值即可. .,
.,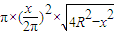 =
=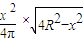
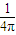 ×(2x×
×(2x×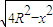 +
+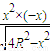 )
)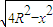 +
+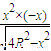 =0,整理得
=0,整理得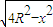 =x,解得x=
=x,解得x=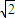 R,此時另一邊長為
R,此時另一邊長為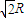
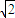 R時,體積取到最大值,最大值為V=
R時,體積取到最大值,最大值為V=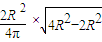 =
=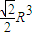
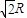 時,此圓柱體體積取到最大值
時,此圓柱體體積取到最大值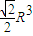


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com