
如圖所示,矩形ABCD的邊AB=a,BC=2,PA⊥平面ABCD,PA=2,現(xiàn)有數(shù)據(jù):①a=![]() ;②a=1;③a=
;②a=1;③a=![]() ;④a=2;⑤a=4.
;④a=2;⑤a=4.
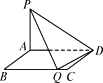
(1)當(dāng)在BC邊上存在點(diǎn)Q,使PQ⊥QD時(shí),a可以取所給數(shù)據(jù)中的哪些值?請(qǐng)說(shuō)明理由;
(2)在滿足(1)的條件下,a取所給數(shù)據(jù)中的最大值時(shí),求直線PQ與平面ADP所成角的正切值;
(3)記滿足(1)的條件下的Q點(diǎn)為Qn(n=1,2,3,…),若a取所給數(shù)據(jù)中的最小值時(shí),這樣的點(diǎn)Qn有幾個(gè)?試求二面角Qn-PA-Qn+1的大小.
|
探究:(1)建立如圖所示空間直角坐標(biāo)系,則A(0,0,0),P(0,0,2),D(0,2,0),
設(shè)Q(a,x,0)(|BQ|=x,0≤x≤2), 于是有 由PQ⊥QD,得 即x2-2x+a=0, 此方程有解,則Δ=4-4a2≥0,∴0≤a≤1. 當(dāng)a= 當(dāng)a=1時(shí),方程的解x=1,也滿足0≤x≤2. 因此,滿足條件的a的取值為a= (2)顯然,在滿足(1)的條件下,a取所給數(shù)據(jù)中的最大值時(shí),a=1,此時(shí),由(1)知x=1,Q(1,1,0)為BC的中點(diǎn), 作QM⊥AD于M,有QM⊥面PAD,M為AD的中點(diǎn), 連接PM,則∠QPM即為PQ與平面PAD所成的角. 在Rt△QMP中,QM=1,PM= ∴tan∠QPM= 即直線PQ與平面ADP所成角的正切值為 (3)在滿足(1)的條件下,a取所給數(shù)據(jù)中的最小值時(shí),a= ∴滿足條件的點(diǎn)Q有兩個(gè):Q1( 此時(shí),所求的二面角應(yīng)為Q1-PA-Q2(如圖所示).
∵PA⊥面ABCD, ∴PA⊥Q1A,PA⊥Q2A, ∴∠Q1AQ2即為所求二面角的平面角, 規(guī)律總結(jié):一般來(lái)說(shuō),設(shè)存在這樣的點(diǎn),然后設(shè)出此點(diǎn)的空間坐標(biāo),轉(zhuǎn)化為代數(shù)上的方程是否有解問(wèn)題,若有解,則存在這樣的點(diǎn),否則,不存在. |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
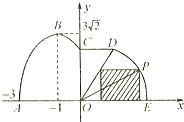 如圖,某市擬在道路的一側(cè)修建一條運(yùn)動(dòng)賽道,賽道的前一部分為曲線段ABC,該曲線段為函數(shù)y=Asin(ωx+φ)(A>0,ω>0,
如圖,某市擬在道路的一側(cè)修建一條運(yùn)動(dòng)賽道,賽道的前一部分為曲線段ABC,該曲線段為函數(shù)y=Asin(ωx+φ)(A>0,ω>0,| π |
| 2 |
| 2 |
| 3 |
 |
| DE |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖所示,在△ABC中,AC=1,AB=3,∠ACB=
如圖所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖所示,在△ABC中,AC=1,AB=3,∠ACB=
如圖所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011年江蘇省南京市金陵中學(xué)高考數(shù)學(xué)預(yù)測(cè)試卷(2)(解析版) 題型:解答題
 <φ<π),x∈[-3,0]的圖象,且圖象的最高點(diǎn)為B(-1,3
<φ<π),x∈[-3,0]的圖象,且圖象的最高點(diǎn)為B(-1,3 );賽道的中間部分為
);賽道的中間部分為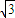 千米的水平跑到CD;賽道的后一部分為以O(shè)圓心的一段圓弧
千米的水平跑到CD;賽道的后一部分為以O(shè)圓心的一段圓弧 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年江蘇省高三預(yù)測(cè)卷2數(shù)學(xué) 題型:解答題
(本小題滿分14分)
如圖,某市擬在道路的一側(cè)修建一條運(yùn)動(dòng)賽道,賽道的前一部分為曲線段ABC,該曲線段為函數(shù)y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的圖象,且圖象的最高點(diǎn)為B(-1,
),x∈[-3,0]的圖象,且圖象的最高點(diǎn)為B(-1, );賽道的中間部分為
);賽道的中間部分為 千米的水平跑到CD;賽道的后一部分為以O(shè)圓心的一段圓弧
千米的水平跑到CD;賽道的后一部分為以O(shè)圓心的一段圓弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圓弧賽道所對(duì)應(yīng)的扇形區(qū)域內(nèi)建一個(gè)“矩形草坪”,如圖所示,矩形的一邊在道路AE上,一個(gè)頂點(diǎn)在扇形半徑OD上.記∠POE= ,求當(dāng)“矩形草坪”的面積最大時(shí)
,求當(dāng)“矩形草坪”的面積最大時(shí) 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com