
(1)在極坐標(biāo)系中,已知圓ρ=2cosθ與直線3ρcosθ+4ρsinθ+a=0相切,求實數(shù)a的值.
(2)對5副不同的手套進行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.對于下列事件:①A:甲正好取得兩只配對手套;②B:乙正好取得兩只配對手套.試判斷事件A與B是否獨立?并證明你的結(jié)論.
(1)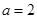 ,或
,或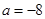 . (2)
. (2) ≠
≠ , A與B是不獨立的.
, A與B是不獨立的.
解析試題分析: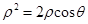 ,圓ρ=2cosθ的普通方程為:
,圓ρ=2cosθ的普通方程為: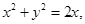 ,即
,即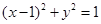
直線3ρcosθ+4ρsinθ+a=0的普通方程為: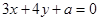 , 4分
, 4分
又圓與直線相切,所以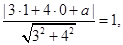
解得: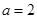 ,或
,或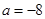 . 7分
. 7分
(2)解:①P(A)=  =
=  ;
;
②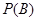 =
= =
=  . 11分
. 11分
∵P(AB)=  =
=  ,
,  =
=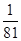 , 13分
, 13分
∴ ≠
≠ ,故A與B是不獨立的. 15分
,故A與B是不獨立的. 15分
考點:本題主要考查極坐標(biāo)方程與直角坐標(biāo)方程的互化,直線與圓的位置關(guān)系,相互獨立事件的概念及其概率計算。
點評:中檔題,本題綜合性較強,覆蓋面較廣。考查知識點注重了基礎(chǔ)。其中(1)化為直角坐標(biāo)方程,利用幾何法研究直線與圓相切問題,是常見方法。相互獨立事件的概率滿足 =
= 。
。


 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知曲線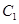 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點, 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .
.
(Ⅰ)把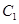 的參數(shù)方程化為極坐標(biāo)方程;
的參數(shù)方程化為極坐標(biāo)方程;
(Ⅱ)求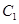 與
與 交點的極坐標(biāo)(
交點的極坐標(biāo)( ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
直角坐標(biāo)系 和極坐標(biāo)系
和極坐標(biāo)系 的原點與極點重合,
的原點與極點重合, 軸正半軸與極軸重合,單位長度相同,在直角坐標(biāo)系下,曲線C的參數(shù)方程為
軸正半軸與極軸重合,單位長度相同,在直角坐標(biāo)系下,曲線C的參數(shù)方程為 為參數(shù))。
為參數(shù))。
(1)在極坐標(biāo)系下,曲線C與射線 和射線
和射線 分別交于A,B兩點,求
分別交于A,B兩點,求 的面積;
的面積;
(2)在直角坐標(biāo)系下,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),求曲線C與直線
為參數(shù)),求曲線C與直線 的交點坐標(biāo)。
的交點坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角坐標(biāo)系 內(nèi),直線
內(nèi),直線 的參數(shù)方程為
的參數(shù)方程為
 為參數(shù)
為參數(shù) .以
.以 為極軸建立極坐標(biāo)系,圓
為極軸建立極坐標(biāo)系,圓 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .判斷直線
.判斷直線 和圓
和圓 的位置關(guān)系.
的位置關(guān)系.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(1)把下列的極坐標(biāo)方程化為直角坐標(biāo)方程(并說明對應(yīng)的曲線):
①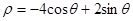 ②
②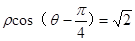
(2)把下列的參數(shù)方程化為普通方程(并說明對應(yīng)的曲線):
③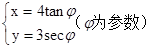 ④
④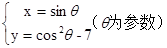
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題共10分)
在直角坐標(biāo)系中直線L過原點O,傾斜角為 ,在極坐標(biāo)系中(與直角坐標(biāo)系有相同的長度單位,極點為原點,極軸與x的非負(fù)半軸重合)曲線C:
,在極坐標(biāo)系中(與直角坐標(biāo)系有相同的長度單位,極點為原點,極軸與x的非負(fù)半軸重合)曲線C: ,
,
(1)求曲線C的直角坐標(biāo)方程;
(2)直線L與曲線C交于點 ,求
,求 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)選修4-4:坐標(biāo)系與參數(shù)方程
已知直線的極坐標(biāo)方程為 ,圓
,圓 的參數(shù)方程為
的參數(shù)方程為 (其中
(其中 為參數(shù)).
為參數(shù)).
(Ⅰ)將直線的極坐標(biāo)方程化為直角坐標(biāo)方程;
(Ⅱ)求圓 上的點到直線的距離的最小值.
上的點到直線的距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
已知極坐標(biāo)系下曲線 的方程為
的方程為 ,直線
,直線 經(jīng)過點
經(jīng)過點 ,傾斜角
,傾斜角 .
.
(Ⅰ)求直線 在相應(yīng)直角坐標(biāo)系下的參數(shù)方程;
在相應(yīng)直角坐標(biāo)系下的參數(shù)方程;
(Ⅱ)設(shè) 與曲線
與曲線 相交于兩點
相交于兩點 ,求點
,求點 到
到 兩點的距離之積.
兩點的距離之積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角坐標(biāo)系 中以
中以 為極點,
為極點, 軸正半軸為極軸建立坐標(biāo)系.圓
軸正半軸為極軸建立坐標(biāo)系.圓 ,直線
,直線 的極坐標(biāo)方程分別為
的極坐標(biāo)方程分別為 .
.
(I)
(II)

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com