解:(1)由題意化簡可知,函數(shù)
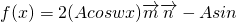
φ=2Acosωx(sinωxcosφ+cosωxsinφ)-Asinφ
=A(sin2ωxcosφ+2cos
2ωxsinφ)-Asinφ=A(sin2ωxcosφ+cos2ωxsinφ)=Asin(2ωx+φ),(4分)
且A=2,
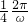
=
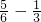
,∴ω=π.
將點P(

,2)代入 y=2sin(πx+φ)可得:sin(

+φ)=1,∴φ=2kπ+

,k∈z.
考慮到

,所以
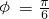
,于是函數(shù)的表達(dá)式為 f(x)=2sin(πx+

). (6分)
(2)由 πx+

=kπ+

k∈z,解得x=k+

.
令

≤k+

≤
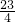
,解得:
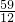
≤k≤

. 由于k∈z,所以k=5.
所以函數(shù)f(x)在區(qū)間
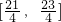
上存在對稱軸,其方程為x=

. …(10分)
分析:(1)由題意利用三角函數(shù)的恒等變換化簡可得函數(shù)f(x)的解析式為 Asin(2ωx+φ),根據(jù)頂點縱坐標(biāo)求出A,據(jù)函數(shù)的周期性求得ω,把點代入求得 φ 的值.
(2)由 πx+

=kπ+

k∈z,解得x=k+

.令

≤k+

≤
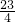
以及k的性質(zhì),解得k的值,從而得出結(jié)論.
點評:本題主要考查三角函數(shù)的恒等變換及化簡求值,兩個向量的數(shù)量積的運算,正弦函數(shù)的對稱性,屬于中檔題.

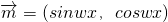 ,
,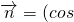 φ,sinφ),函數(shù)
φ,sinφ),函數(shù)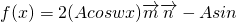 φ (其中
φ (其中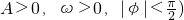 的圖象在y軸右側(cè)的第一個最高點(即函數(shù)取得最大值的點)為P(
的圖象在y軸右側(cè)的第一個最高點(即函數(shù)取得最大值的點)為P( ,2),在原點右側(cè)與x軸的第一個交點為Q(
,2),在原點右側(cè)與x軸的第一個交點為Q( ,0).
,0).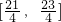 上是否存在對稱軸,存在求出方程;否則說明理由.
上是否存在對稱軸,存在求出方程;否則說明理由.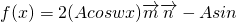 φ=2Acosωx(sinωxcosφ+cosωxsinφ)-Asinφ
φ=2Acosωx(sinωxcosφ+cosωxsinφ)-Asinφ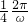 =
=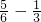 ,∴ω=π.
,∴ω=π. ,2)代入 y=2sin(πx+φ)可得:sin(
,2)代入 y=2sin(πx+φ)可得:sin( +φ)=1,∴φ=2kπ+
+φ)=1,∴φ=2kπ+ ,k∈z.
,k∈z. ,所以
,所以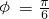 ,于是函數(shù)的表達(dá)式為 f(x)=2sin(πx+
,于是函數(shù)的表達(dá)式為 f(x)=2sin(πx+ ). (6分)
). (6分) =kπ+
=kπ+ k∈z,解得x=k+
k∈z,解得x=k+ .
. ≤k+
≤k+ ≤
≤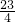 ,解得:
,解得: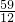 ≤k≤
≤k≤ . 由于k∈z,所以k=5.
. 由于k∈z,所以k=5.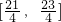 上存在對稱軸,其方程為x=
上存在對稱軸,其方程為x= . …(10分)
. …(10分) =kπ+
=kπ+ k∈z,解得x=k+
k∈z,解得x=k+ .令
.令  ≤k+
≤k+ ≤
≤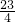 以及k的性質(zhì),解得k的值,從而得出結(jié)論.
以及k的性質(zhì),解得k的值,從而得出結(jié)論.

 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案 (2012•西城區(qū)二模)已知函數(shù)f(x)=sin(ωx+φ)+
(2012•西城區(qū)二模)已知函數(shù)f(x)=sin(ωx+φ)+