（本題滿分共13分）已知函數
（1）求函數
的單調遞減區間；（2）當
時，函數
在
有零點，求
的最大值。
科目：高中數學 來源： 題型：
（本題滿分共12分）某流感病研究中心對溫差與甲型H1N1病毒感染數之間的相關關系進行研究，他們每天將實驗室放入數量相同的甲型H1N1病毒和100頭豬，然后分別記錄了4月1日至4月5日每天晝夜溫差與實驗室里100頭豬的感染數，得到如下資料：
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 溫 差 | 10 | 13 | 11 | 12 | 7 |
| 感染數 | 23 | 32 | 24 | 29 | 17 |
（1）求這5天的平均感染數；（2）從4月1日至4月5日中任取2天，記感染數分別為
用
的形式列出所有的基本事件， 其中
視為同一事件,并求
的事件A的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
（本題滿分共13分）已知正項數列
，函數
。（1）若正項數列
滿足
（
且
），試求出
由此歸納出通項
，并證明之；（2）若正項數列滿足
（且
），數列
滿足
，其和為
，求證
。
查看答案和解析>>
科目：高中數學 來源：2011-2012學年湖南省四市九校高三上學期12月月考文科數學 題型：解答題
（本題滿分13分）已知橢圓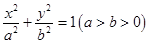
的離心率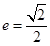
，短軸長為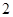
（Ⅰ）求橢圓方程；
（Ⅱ）若橢圓與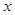
軸正半軸、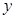
軸正半軸的交點分別為
、
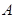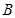，經過點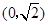
且斜率k的直線
與橢圓交于不同的兩點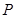
、
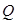，是否存在常數
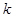，使得向量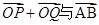
共線？如果存在，求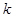的值；如果不存在，請說明理由。
查看答案和解析>>
科目：高中數學 來源：2014屆湖南省高一12月月考數學 題型：解答題
（本題滿分13分）如圖，線段
，
所在直線是異面直線，
，
，
，
分別是線段
，
，
，
的中點．
（１） 求證：
共面且
面，
面；
（２） 設
，
分別是和上任意一點，求證：
被平面平分．
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
時，遞減區間為
當
時 不存在 當
時 遞減區間為
(Ⅱ) 
的最大值
即 
時 
令
得
或
）
時，
內不存在零點。
時 
時 
在
內存在一零點。故當函數
在
有零點時，
