
 (S2n+S2m)-(n-m)2,其中m,n為任意正整數.
(S2n+S2m)-(n-m)2,其中m,n為任意正整數. -
- an+33=k2的所有正整數k,n.
an+33=k2的所有正整數k,n. (S2n+S2m)-(n-m)2中,分別令m=1,m=2,得
(S2n+S2m)-(n-m)2中,分別令m=1,m=2,得 (S2n+S2)-(n-1)2,①
(S2n+S2)-(n-1)2,① (S2n+S4)-(n-2)2,②
(S2n+S4)-(n-2)2,②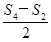 .(3分)
.(3分) (S2n+S2m)-(n-m2)中,令n=1,m=2,得S3=
(S2n+S2m)-(n-m2)中,令n=1,m=2,得S3= (S2+S4)-1,由題設知,S2=11,S3=19,故S4=29.
(S2+S4)-1,由題設知,S2=11,S3=19,故S4=29.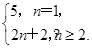 (5分)
(5分) 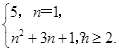 即Sn=n2+3n+1,n∈N*.(6分)
即Sn=n2+3n+1,n∈N*.(6分) -
- an+33=k2(*).
an+33=k2(*).

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源:不詳 題型:解答題
 =an+1-
=an+1- n2-n-
n2-n- ,n∈N*.
,n∈N*. .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 |  |  |
 |  |  |
 |  |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com